
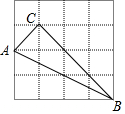
 如图,在4×4的方格纸中,每个小方格的边长都是1,△ABC的三个顶点分别在方格的格点上.
如图,在4×4的方格纸中,每个小方格的边长都是1,△ABC的三个顶点分别在方格的格点上.分析 (1)由矩形的面积减去三个直角三角形的面积即可;
(2)由勾股定理和勾股定理的逆定理证出△ABC是直角三角形,再由三角形面积关系即可得出结果.
解答 解:(1)△ABC的面积=3×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×1=3;
(2)∵AC2=12+12=2,BC2=32+32=18,AB2=22+42=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴AB边上的高=$\frac{AC•BC}{AB}$=$\frac{\sqrt{2}×3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
点评 此题考查了勾股定理与勾股定理的逆定理.此题比较简单,解题的关键是掌握勾股定理与勾股定理的逆定理的应用,掌握数形结合思想的应用.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
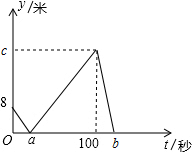 甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.
甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com