
分析 等腰三角形的一条腰上的高等于该三角形一边的一半,既没有说明该等腰三角形是锐角三角形还是钝角三角形,又没有说明是等于腰长还底边的一半,因此需分三种情况,进行分类讨论.
解答 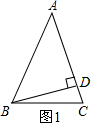 解:(1)当等腰三角形腰上的高等于腰长的一半时:
解:(1)当等腰三角形腰上的高等于腰长的一半时:
①如图1,当等腰三角形为锐角三角形时:
∵BD⊥AC,且AC=AB=2BD,
∴∠A=30°,
∴∠ABC=∠C=75°;
即等腰三角形的底角为75°,
②如图2,当等腰三角形为钝角三角形时: ∵BD⊥AC,且AC=AB=2BD,
∵BD⊥AC,且AC=AB=2BD,
∴∠DAB=30°,
∴∠CAB=150°,
∴∠C=∠ABC=15°,
即等腰三角形的底角为15°;
(2)当等腰三角形腰上的高等于底的一半时: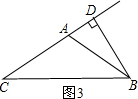
∵BD⊥AC,且CB=2BD,
∴∠C=30°,
即等腰三角形的顶角为30°.
综上所述,等腰三角形的一条腰上的高等于该三角形一边的一半时,其底角度数可能是30°,15°,75°.
故答案为:30°,15°,75°.
点评 本题考查了等腰三角形的性质;在解决与等腰三角形有关的问题,由于等腰所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一个半径为r的圆形纸片在边长为a(a>$2\sqrt{2}r$)的正方形内任意运动,则在该正方形内,这个圆形纸片“接触不到的部分”的面积是( )
如图,一个半径为r的圆形纸片在边长为a(a>$2\sqrt{2}r$)的正方形内任意运动,则在该正方形内,这个圆形纸片“接触不到的部分”的面积是( )| A. | $\frac{π}{4}{r}^{2}$ | B. | $\frac{4-π}{4}{r}^{2}$ | C. | (4-π)r2 | D. | πr2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ABC=90°,以AB为直径作⊙O交斜边AC于点D,过点D作⊙O的切线DE交BC于点E.
如图,△ABC中,∠ABC=90°,以AB为直径作⊙O交斜边AC于点D,过点D作⊙O的切线DE交BC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com