
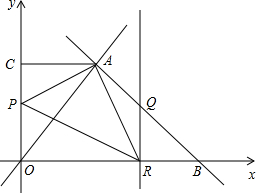
 如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.
如图,已知直线y=-x+7与直线y=$\frac{4}{3}$x交于点A,且与x轴交于点B,过点A作AC⊥y轴与点C.点P从O点以每秒1个单位的速度沿折线O-C-A运动到A;点R从B点以相同的速度向O点运动,一个点到终点时,另一个点也随之停止运动.分析 (1)联立两直线的解析式求出点A的坐标,利用x轴上点的坐标特征,求出点B的坐标;
(2)利用面积的差得出四边形APOR的面积为-$\frac{1}{2}$t+14=13求出t即可;
(3)假设存在,分三种情况讨论计算即可.
解答 解:(1)∵直线y=-x+7①与直线y=$\frac{4}{3}$x②交于点A,
∴联立①②解得,x=3,y=4,
∴A(3,4),
令y=-x+7中,y=0,得,x=7,
∴B(7,0);
(2)由运动知,BR=t,
∵过R的直线l∥y轴,且与线段BA相交,
∴0≤t≤4,
∴OR=7-t,
∵AC⊥y轴,
∴OC=4,
∴点P必在线段OC上,
由运动知,OP=t,∴CP=4-t,
①S四边形APOR=S四边形ACOB-S△ACP-S△ABR
=$\frac{1}{2}$(AC+OB)×OC-$\frac{1}{2}$AC×CP-$\frac{1}{2}$BR×OC
=$\frac{1}{2}$(3+7)×4-$\frac{1}{2}$×3×(4-t)-$\frac{1}{2}$×t×4
=20-6+$\frac{3}{2}$t-2t
=-$\frac{1}{2}$t+14,
∵以A,P,O,R为顶点的四边形的面积为13,
∴-$\frac{1}{2}$t+14=13,
∴t=2;
②∴P(0,t),R(7-t,0),
∵A(3,4),
∴PA2=9+(t-4)2,PR2=(7-t)2+t2,RA2=(7-t-3)2+16=(t-4)2+16,
假设存在以A、P、R为顶点的三角形是等腰三角形,
∴①当PA=PR时,即:PA2=PR2,
∴9+(t-4)2=(7-t)2+t2,
∴t2-6t+24=0,此方程无解,
②当PA=RA时,即:PA2=RA2,
∴9+(t-4)2=(t-4)2+16,明显,此方程无解,
③当PR=RA时,即:PR2=RA2,
∴(7-t)2+t2=(t-4)2+16,
∴t2-6t+17=0,此方程无解,
∴不存在以A、P、R为顶点的三角形是等腰三角形.
点评 此题是一次函数综合题,主要考查了直线的交点坐标的求法,四边形的面积的计算方法,等腰三角形的性质,解本题的关键是分类讨论的思想解决问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
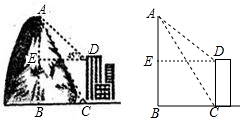 某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)
某乡镇中学教学活动小组,为测量数学楼后面的山高AB,用了如下方法.如图所示,在教学楼底C处测得山顶A的仰角为60°,在教学楼顶D处,测得山顶A的俯角为45°.已知教学楼高CD=12米,求山高AB.(结果可化为最简根式)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
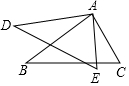 如图,请看以下两个推理过程:
如图,请看以下两个推理过程:| A. | ①对②错 | B. | ①错②对 | C. | ①②都对 | D. | ①②都错 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-3(m>0)与x轴的交点为A,B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
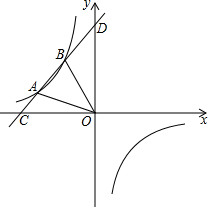 如图,直线y=mx+n(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A、B两点,直线AB与坐标轴分别交于C、D两点,连接OA,若OA=2$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B(-3,b).
如图,直线y=mx+n(m≠0)与双曲线y=$\frac{k}{x}$(k≠0)交于A、B两点,直线AB与坐标轴分别交于C、D两点,连接OA,若OA=2$\sqrt{10}$,tan∠AOC=$\frac{1}{3}$,点B(-3,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com