
分析 通过观察可知,规律是根号外的符号以及根号下的被开方数依次是:(-1)1+1×0,(-1)2+1 $\sqrt{3}$,(-1)3+1 $\sqrt{3×2}$…,(-1)n+1 $\sqrt{3(n-1)}$,可以得到第14个的答案.
解答 解:由题意知道:题目中的数据可以整理为:(-1)1+1×0,(-1)2+1 $\sqrt{3}$,(-1)3+1 $\sqrt{3×2}$…,(-1)n+1 $\sqrt{3(n-1)}$,
∴第13个答案为:(-1)14+1 $\sqrt{3×(14-1)}$=-$\sqrt{39}$.
故答案为:-$\sqrt{39}$.
点评 此题主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG
如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG查看答案和解析>>
科目:初中数学 来源: 题型:解答题
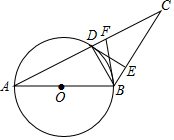 如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.
如图,在⊙O中,直径AB=8,∠A=30°,AC=8$\sqrt{3}$,AC与⊙O交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com