
【题目】如图①,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求抛物线的函数解析式;
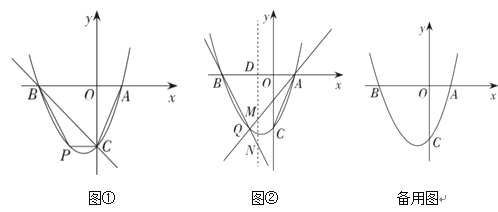
(2)如图①,点![]() 在第三象限内的抛物线上.
在第三象限内的抛物线上.
①连接![]() ,
,![]() ,
,![]() ,当四边形
,当四边形![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
②![]() 为
为![]() 轴上一点,当
轴上一点,当![]() 取得最小值时,求点
取得最小值时,求点![]() 的坐标;
的坐标;
(3)如图②,![]() 为
为![]() 轴下方抛物线上任意一点,
轴下方抛物线上任意一点,![]() 是抛物线的对称轴与
是抛物线的对称轴与![]() 轴的交点,直线
轴的交点,直线![]() ,
,![]() 分别交抛物线的对称轴于点
分别交抛物线的对称轴于点![]() ,
,![]() .问:
.问:![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)y=x2+2x-3;(2)①![]() ,②
,②![]() ;(3)DM+DN是定值,定值为8.
;(3)DM+DN是定值,定值为8.
【解析】
(1)由直线表达式求出点B、C的坐标,将A、B、C坐标代入抛物线表达式,即可求解;
(2)①S四边形ABPC=S△BPC+S△ABC=![]() PFOB+
PFOB+![]() ABOC=
ABOC= ![]() (-t2-3t)+6=
(-t2-3t)+6=![]() (t+
(t+![]() )2+
)2+![]() ,即可求解;②当GJ=
,即可求解;②当GJ=![]() AG时,PG+
AG时,PG+![]() AG取得最小值,即可求解;
AG取得最小值,即可求解;
(3)利用![]() ,
,![]() ,得
,得![]() ,
,![]() ,即
,即![]() ,
,![]() ,即可求解.
,即可求解.
解:(1)在y=-x-3中,令x=0,得y=-3;令y=0,得x=-3,
∴B(-3,0),C(0,-3).
设抛物线的函数解析式为y=a(x+3)(x-1),
将点C(0,-3)代入,得a=1,
∴抛物线的函数解析式为y=x2+2x-3;
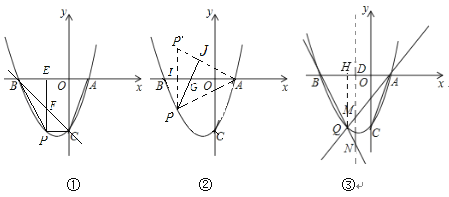
(2)①如图①,过点P作PE⊥x轴于点E,交BC于点F,设点P的坐标为(t,t2+2t-3),则点F的坐标为(t,-t-3),
∴PF=-t-3-(t2+2t-3)=-t2-3t,
∴S四边形ABPC=S△BPC+S△ABC=![]() PF·OB+
PF·OB+![]() AB·OC=
AB·OC=![]() (-t2-3t)+6=
(-t2-3t)+6=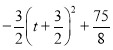 .
.
∵![]() <0,
<0,
∴当t=![]() 时,S四边形ABPC取得最大值,
时,S四边形ABPC取得最大值,
∴此时点P的坐标为![]() ;
;
②如图②,作点P关于x轴的对称点![]() ,
,![]() 交x轴于点I,连接AP,
交x轴于点I,连接AP,![]() ,过点P作PJ⊥
,过点P作PJ⊥![]() 于点J,交x轴于点G.当GJ=
于点J,交x轴于点G.当GJ=![]() AG时,PG+
AG时,PG+![]() AG取得最小值,此时sin∠GAJ=
AG取得最小值,此时sin∠GAJ=![]() ,
,
∴tan∠GAJ=![]() .
.
设点P的坐标为(t,t2+2t-3),则PI=-t2-2t+3,AI=-t+1,
由对称的性质,得∠PAI=∠GAJ,
∴tan∠PAI=![]() ,即
,即![]() ,
,
解得t1=![]() ,t2=1(舍去),
,t2=1(舍去),
∴此时点P的坐标为![]() ;
;
(3)DM+DN是定值.
解法一:如图③,过点Q作QH⊥x轴于点H.
∵ND⊥x轴,
∴QH∥ND,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设点Q的坐标为(k,k2+2k-3),则HQ=-k2-2k+3,BH=3+k,AH=1-k.
∵D是抛物线的对称轴与x轴的交点,
∴AD=BD=2,
∴![]() ,
,![]() ,
,
∴DN=2-2k,DM=2k+6,
∴DM+DN=2k+6+2-2k=8,
∴DM+DN是定值,该定值为8.
解法二:∵抛物线y=x2+2x-3的对称轴为x=-1,
∴D(-1,0),则xM=xN=-1.
设点Q的坐标为(k,k2+2k-3),
设直线AQ的解析式为y=dx+e,则![]() ,解得
,解得![]() ,
,
∴直线AQ的解析式为y=(k+3)x-k-3,
当x=-1时,y=-2k-6,
∴DM=2k+6.
设直线BQ的解析式为y=mx+n,则![]() ,解得
,解得![]() ,
,
∴直线BQ的解析式为y=(k-1)x+3k-3,
当x=-1时,y=2k-2,
∴DN=-2k+2,
∴DM+DN=2k+6+(-2k+2)=8,
∴DM+DN是定值,该定值为8.


科目:初中数学 来源: 题型:
【题目】五张正面分别写有数字:﹣3,﹣2,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不小于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为m的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为n的值,请用列表法或画树状图法,求点Q(m,n)在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
与x轴相交于A、B两点(A左B右),与y轴交于点C.其顶点为D.
(1)求点D的坐标和直线BC对应的一次函数关系式;
(2)若正方形PQMN的一边PQ在线段AB上,另两个顶点M、N分别在BC、AC上,试求M、N两点的坐标;
(3)如图1,E是线段BC上的动点,过点E作DE的垂线交BD于点F,求DF的最小值.
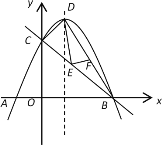
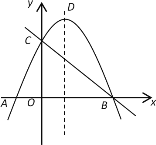
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信息快速发展的新时代,“信息消费”已成为人们生活的重要部分.为了解某社区居民每月信息消费的情况,学校社会实践小组到该社区随机调查了部分住户2019年7月的信息消费金额,并将手机到的数据整理成不完整统计图(图9.1、图9.2).
请结合图中相关数据回答下列问题.

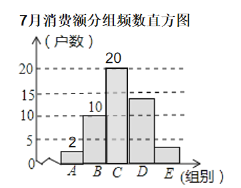

(1)本次调查样本的容量是______;
(2)D组的频数是______,E组的频率是______,B组所对应扇形的圆心角为______度;
(3)在调查的住户中,当月信息消费金额的中位数出现在______组;
(4)若该社区有1500户住户,估计当月信息消费额不少于300元的约有______户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,新型冠状病毒席卷全球,疫情当前,全国上下砥砺同行.某中学校指导中心为引导未成年人以健康心理、阳光心态抗击疫情,积极开展了心理援助工作,并推出“你是我的奥特曼”有奖征稿活动.活动结束后,该指导中心对参赛学生的获奖情况进行统计,并绘制了如下两幅不完整的统计图.
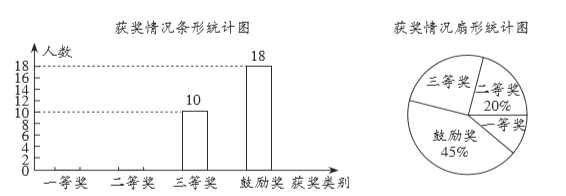
结合图中的相关数据,解答下列问题:
(1)参加此次有奖征稿活动的学生有 人,在扇形统计图中,“三等奖”所对应扇形的圆心角度数为 ;
(2)将条形统计图补充完整;
(3)若获得“一等奖”的学生中有![]() 来自七年级,
来自七年级,![]() 来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
来自九年级,其余来自八年级,学校决定从获得“一等奖”的学生中任选2名作为代表在线上分享心灵战“疫”小锦囊,请用列表或画树状图的方法求所选2名学生中恰好是1名七年级和1名九年级学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)设种植的总成本为w元,
①求w与x之间的函数关系式;
②若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
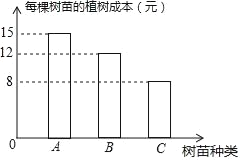
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚一起做游戏,游戏规则如下:将分别标有数字 1, 2, 3, 4 的 4 个小球放入一个不透明的袋子中,这些球除数字外都相同.从中随机摸出一个球记下数字后放回,再从中随机摸出一个球记下数字.若两次数字差的绝对值小于 2,则小明获胜,否则小刚获胜.这个游戏对两人公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
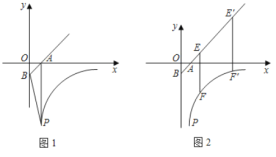
【题目】如图1,直线y=x-1交x轴、y轴于A、B点,点P(1,![]() ,且S四边形PAOB=3.5,双曲线y=
,且S四边形PAOB=3.5,双曲线y=![]() 经过点P.
经过点P.
(1)求k的值;
(2)如图2,直线![]() )交射线BA于E,交双曲线y=
)交射线BA于E,交双曲线y=![]() 于F,将直线
于F,将直线![]() 向右平移4个单位长度后交射线于
向右平移4个单位长度后交射线于![]() ,交双曲线y=
,交双曲线y=![]() 于
于![]() ,若
,若![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
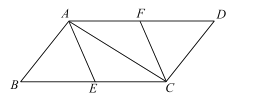
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com