
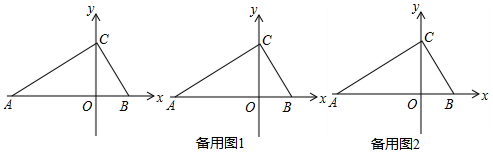
分析 (1)如图1中,根据直角三角形30度角性质,可知BC=2OB,AB=2BC,求出OA即可解决问题.
(2)分两种情形①如图2中,当0<t≤2时,②如图3中,当t>2时,分别求解即可.
(3)如图4中,作AN⊥DP交DP的延长线于N,OM⊥AD于M.首先证明△ANP≌△EMO,推出PN=OM,再由$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•OA•OC,求出OM=$\frac{2\sqrt{3}•6}{4\sqrt{3}}$=3,PN=3,推出点P的横坐标为-3,求出点P(-3,5$\sqrt{3}$),PB=$\sqrt{(-3-2)^{2}+(5\sqrt{3})^{2}}$=10,t=5,根据(2)中的结论即可解决问题.
解答 解:(1)如图1中,
∵CA⊥CB,
∴∠ACB=90°,
∵∠CBO=60°,∠BOC=90°,
∴∠A=∠BCO=30°,∵B(2,0),
∴OB=2,BC=2OB=4,AB=2BC=8,
∴OA=AB-OB=6,
∴A(-6,0).
(2)①如图2中,当0<t≤2时,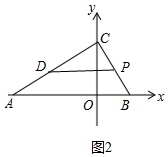
在RT△DPC中,∵∠DCP=90°,DP∥AB,
∴∠CDP=∠A=30°,
∴d=DP=2PC=2(4-2t)=8-4t.
②如图3中,当t>2时,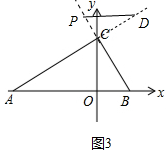
在Rt△PCD中,同理可得d=PD=2PC=2(2t-4)=4t-8,
综上所述,d=$\left\{\begin{array}{l}{8-4t}&{(0<t≤2)}\\{4t-8}&{(t>2)}\end{array}\right.$.
(3)如图4中,作AN⊥DP交DP的延长线于N,OM⊥AD于M.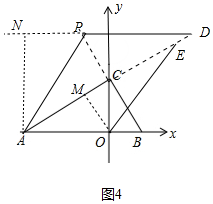
∵∠CEO+∠PAB=90°,∠PAB+∠NAP=90°,
∴∠PAN=∠OEM,∵AP=OE,∠ANP=∠OME=90°,
∴△ANP≌△EMO,
∴PN=OM,
∵$\frac{1}{2}$•AC•OM=$\frac{1}{2}$•OA•OC,
∴OM=$\frac{2\sqrt{3}•6}{4\sqrt{3}}$=3,
∴PN=3,
∴点P的横坐标为-3,
∵B(2,0),C(0,2$\sqrt{3}$),
∴直线BC的解析式为y=-$\sqrt{3}$x+2$\sqrt{3}$,
∴P(-3,5$\sqrt{3}$),
∴PB=$\sqrt{(-3-2)^{2}+(5\sqrt{3})^{2}}$=10,
∴t=5,
∴d=4t-8=20-8=12.
点评 本题考查三角形综合题、直角三角形30度角性质、全等三角形的判定和性质、勾股定理,等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用面积法求线段的长,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{DE}{BC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{3}$ | C. | $\frac{AE}{AC}$=$\frac{1}{2}$ | D. | $\frac{AE}{AC}$=$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有理数包括正数、零和负数 | |
| B. | -a2一定是负数 | |
| C. | 34.37°=34°22′12″ | |
| D. | 两个有理数的和一定大于每一个加数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
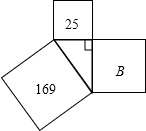 如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:
如图所示.以直角三角形的三条边为边长分别作正方形.依据图中所给条件,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
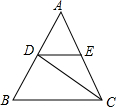 如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )
如图,△ABC中,AB=AC=BC,CD是∠ACB的平分线,过D作DE∥BC交AC于E,若△ABC的边长为a,则△ADE的周长是( )| A. | 2a | B. | $\frac{4}{3}$a | C. | $\frac{3}{2}$a | D. | a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,小明家(点P)与限速60千米/小时的高速公路AB之间有一块巨型广告牌CD,已知小明家距离高速公路60米,在△ABP中,∠A=60°,∠B=45°,一辆车自西向东匀速行驶,小明从P处观察,看到它在A处消失9秒后又在B处出现,请问这辆车经过AB段是否超速?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
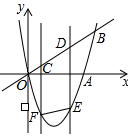 如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.
如图,二次函数y=x2-4x的图象与x轴、直线y=x的一个交点分别为点A、B,CD是线段OB上的一动线段,且CD=2,过点C、D的两直线都平行于y轴,与抛物线相交于点F、E,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{250+90}{x}$$-\frac{250}{x(1+80%)}$=2.5 | B. | $\frac{250+90}{x(1-80%)}$$-\frac{250}{x}$=2.5 | ||
| C. | $\frac{250+90}{80%}$$-\frac{250}{x}$=2.5 | D. | $\frac{250+90}{x}$$-\frac{250}{80%x}$=2.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com