
【题目】如图,已知![]() ,射线
,射线![]() .
.

![]() 请画出
请画出![]() 的平分线
的平分线![]() ;
;
![]() 如果
如果![]() ,射线
,射线![]() 分别表示从点
分别表示从点![]() 出发东、西两个方向,那么射线
出发东、西两个方向,那么射线![]() 方向,射线
方向,射线![]() 表示 方向.
表示 方向.
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,在图中找出所有与
时,在图中找出所有与![]() 互补的角,这些角是_ .
互补的角,这些角是_ .
【答案】(1)详见解析;(2)北偏东20°,北偏西35°;(3)![]()
【解析】
(1)以点O为圆心,以任意长为半径画弧,与OB、ON相交于两点,再分别以这两点为圆心,以大于它们![]() 长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;
长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;
(2)过点O作OE⊥AB,根据垂直的定义以及角平分线的定义求出∠EON与∠COE,然后根据方位角的定义解答即可;
(3)根据∠AON=60°,利用平角的定义可得∠BON,利用角平分线的定义求出∠CON=60°,然后求出∠AOC=120°从而得解.
解:(1)如图所示,OC即为∠BON的平分线;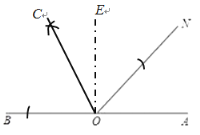
(2)过点O作OE⊥AB,
∵∠AON=70°,
∴∠EON=90°-70°=20°,
∴ON是北偏东20°,
∵OC平分∠BON,
∴∠CON=![]() (180°-70°)=55°,
(180°-70°)=55°,
∴∠COE=∠CON-∠EON=55°-20°=35°,
∴OC是北偏西35°;
故答案为:北偏东20°;北偏西35°.
(3)∵∠AON=60°,OC平分∠BON,
∴∠CON=![]() (180°-60°)=60°,
(180°-60°)=60°,
∴∠AOC=∠CON+∠AON=60°+60°=120°,
∴∠AOC+∠AON=180°,
又根据平角的定义得,∠BON+∠AON=180°,
∴与∠AON互补的角有∠AOC,∠BON;
故答案为:∠AOC,∠BON.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A、B(A点在B点的左侧)与y轴交于点C。
与x轴交于A、B(A点在B点的左侧)与y轴交于点C。
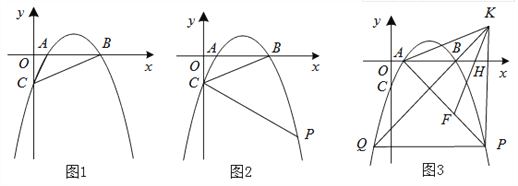
(1)如图1,连接AC、BC,求△ABC的面积。
(2)如图2:
①过点C作CR∥x轴交抛物线于点R,求点R的坐标;
②点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的坐标。
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=![]() ,连接KB并延长交抛物线于点Q,求PQ的长。
,连接KB并延长交抛物线于点Q,求PQ的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过点(3,2)和(1,4).
(1)画出此函数的图象;
(2)求此一次函数的表达式;
(3)若此函数的图象与x轴交于点A,与y轴交于点B,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2a2)3+2a2a4﹣a8÷a2
(2)﹣12018﹣(![]() )﹣2+(﹣3)0
)﹣2+(﹣3)0
(3)2a(a﹣b)(a+2b)
(4)(﹣3m+2n)(﹣2n﹣3m)(9m2﹣4n2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, ![]() m)(m为非负数),则CA+CB的最小值是_____.
m)(m为非负数),则CA+CB的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为

A.(1.4,-1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=![]() +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com