
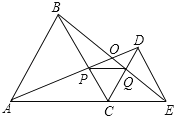
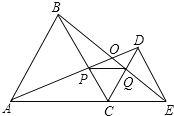
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
【答案】①②③⑤
【解析】
试题分析:由已知条件运用等边三角形的性质得到三角形全等,进而得到更多结论,然后运用排除法,对各个结论进行验证从而确定最后的答案.
解:①∵正△ABC和正△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∵∠ACD=∠ACB+∠BCD,∠BCE=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠ADC=∠BEC,(故①正确);
②又∵CD=CE,∠DCP=∠ECQ=60°,∠ADC=∠BEC,
∴△CDP≌△CEQ(ASA).
∴CP=CQ,
∴∠CPQ=∠CQP=60°,
∴∠QPC=∠BCA,
∴PQ∥AE,(故②正确);
③∵△CDP≌△CEQ,
∴DP=QE,
∵△ADC≌△BEC
∴AD=BE,
∴AD﹣DP=BE﹣QE,
∴AP=BQ,(故③正确);
④∵DE>QE,且DP=QE,
∴DE>DP,(故④错误);
⑤∠AOB=∠DAE+∠AEO=∠DAE+∠ADC=∠DCE=60°,(故⑤正确).
∴正确的有:①②③⑤.
故答案为:①②③⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点A、B、C在数轴上表示的数a、b、c满足(b+3)2+|c﹣24|=0,且多项式x|a+3|y2﹣ax3y+xy2﹣1是五次四项式.
(1)分别求a、b、c的值;
(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以3个单位/秒的速度向右运动,同时点Q从点C出发,以7个单位/秒的速度向左运动:
①若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;
②若点P运动到点B处,动点Q再出发,则P运动几秒后这两点之间的距离为5个单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽做一道数学题:“已知两个多项式A,B,B为 ![]() ﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是
﹣5x﹣6,求A+B”.小丽把A+B看成A﹣B,计算结果是 ![]() +10x+12.根据以上信息,你能求出A+B的结果吗?
+10x+12.根据以上信息,你能求出A+B的结果吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数是3,BC上的数是7,CD上的数是12,则AD上的数是( )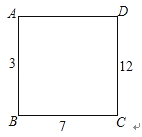
A.2
B.7
C.8
D.15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com