
| A. | $\frac{900}{x}$=$\frac{600}{x+30}$ | B. | $\frac{900}{x}$=$\frac{600}{x-30}$ | C. | $\frac{600}{x}$=$\frac{900}{x+30}$ | D. | $\frac{600}{x}$=$\frac{900}{x-30}$ |
分析 根据A、B两种机器人每小时搬运化工原料间的关系可得出A型机器人每小时搬运化工原料(x+30)千克,再根据A型机器人搬运900千克所用时间与B型机器人搬运600千克所用时间相等即可列出关于x的分式方程,由此即可得出结论.
解答 解:设B型机器人每小时搬运化工原料x千克,则A型机器人每小时搬运化工原料(x+30)千克,
∵A型机器人搬运900千克所用时间与B型机器人搬运600千克所用时间相等,
∴$\frac{600}{x}=\frac{900}{x+30}$.
故选C.
点评 本题考查了由实际问题抽象出分式方程,解题的关键是根据数量关系列出关于x的分式方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程是关键.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=2,x2=1 | B. | x1=$\frac{1}{2}$,x2=1 | C. | x1=-2,x2=1 | D. | x1=-$\frac{1}{2}$,x2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
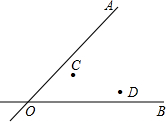 如图,两条公路OA、OB相交于点O,在∠AOB内部有两个村庄C、D,现要在∠AOB内部修建一个水库P,使得该水库到两条公路OA、OB距离相等,且到两个村庄C、D的距离也相等.请通过尺规作图确定水库P的位置.(要求:不写作法,保留作图痕迹,写出结论)
如图,两条公路OA、OB相交于点O,在∠AOB内部有两个村庄C、D,现要在∠AOB内部修建一个水库P,使得该水库到两条公路OA、OB距离相等,且到两个村庄C、D的距离也相等.请通过尺规作图确定水库P的位置.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
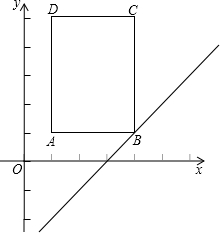 如图,矩形ABCD在平面直角坐标系中,点A(1,1),B(4,1),C(4,5),D(1,5),将一次函数y=x-3的图象L沿y轴以每秒1个单位的速度向上运动,设运动的时间为t秒,L扫过矩形的面积为S.
如图,矩形ABCD在平面直角坐标系中,点A(1,1),B(4,1),C(4,5),D(1,5),将一次函数y=x-3的图象L沿y轴以每秒1个单位的速度向上运动,设运动的时间为t秒,L扫过矩形的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论:①b2>4ac;②ac>0; ③a-b+c>0; ④不等式ax2+bx+c>0的解集是-1<x<3;⑤当x>1时,y随x的增大而减小,其中结论正确的序号是( )| A. | ①②③ | B. | ①④⑤ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com