

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题



查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
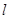 . 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东
. 救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号. 他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙. 乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东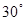 方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
方向,甲、乙的游泳速度均是2米/秒.问谁先到达B处?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com