
分析 根据|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,可知|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,然后分两种情况讨论即可.
解答 解:∵|a-b|≤9,|c-d|≤16,且|a-b-c+d|=25,
∴|a-b|=9,|c-d|=16,且a-b和c-d的符号是相反的,
∴①a-b=9,c-d=-16,此时|b-a|-|d-c|=|-9|-|16|=9-16=-7,
②a-b=-9,c-d=16,此时|b-a|-|d-c|=|9|-|-16|=9-16=-7,
综上所述,|b-a|-|d-c|的值为-7.
点评 本题主要考查绝对值,解决此题时,关键在于确定出a-b和c-d的值,根据其值计算即可.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
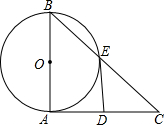 已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,
已知,在Rt△ABC中,∠BAC=90°,以AB为直径的⊙O与BC相交于点E,在AC上取一点D,使得DE=AD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 4,5,6 | C. | 6,8,11 | D. | 5,12,20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | $-3\sqrt{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{b}{a}=\frac{bc}{ac}$ | B. | $\frac{b}{a}=\frac{b+c}{a+c}$ | C. | $\frac{b}{a}=\frac{b^2}{a^2}$ | D. | $\frac{b}{a}=\frac{ab}{a^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com