
【题目】在平面直角坐标系xOy中,已知点 ![]() 、点
、点 ![]() ,一次函数
,一次函数 ![]() 的图象与直线
的图象与直线 ![]() 交于点
交于点 ![]() .
.
(1)求直线 ![]() 的函数解析式及
的函数解析式及 ![]() 点的坐标;
点的坐标;
(2)若点 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积为6,求点
的面积为6,求点 ![]() 的坐标.
的坐标.
【答案】
(1)
解:设直线 ![]() 的函数解析式为
的函数解析式为 ![]() (
( ![]() ).
).
由点 ![]() 、点
、点 ![]() 可得:
可得:
![]()
解得 ![]()
∴直线 ![]() 的函数解析式为
的函数解析式为 ![]() .
.
由 ![]() 得:
得: ![]()
∴ ![]() 点的坐标为
点的坐标为 ![]()
(2)
解:由已知可设点 ![]() 的坐标为
的坐标为 ![]() .
.
∵△ ![]() 的面积为6,
的面积为6,
∴ ![]() .
.
∴ ![]() .
.
∴ ![]() ,或
,或 ![]() .
.
∴点 ![]() 的坐标为
的坐标为 ![]() 或
或 ![]()
【解析】(1)设直线 A B 的函数解析式为 y = k x + b ( k ≠ 0 ).
将 ![]() 、
、 ![]() 代入得:
代入得:![]() 解此方程即可得 直线
解此方程即可得 直线 ![]() 的函数解析式 .
的函数解析式 .
再联立 ![]() 即可得
即可得![]()
![]()
![]()
(2)设 ![]()
![]() .由三角形面积得
.由三角形面积得![]() 解之即可得点
解之即可得点![]()
![]() 或
或 ![]()
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握三角形的面积(三角形的面积=1/2×底×高)的相关知识才是答题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.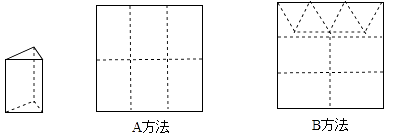
现有19张硬纸板,裁剪时 ![]() 张用A方法,其余用B方法.
张用A方法,其余用B方法.
(1)分别求裁剪出的侧面和底面的个数(用含 ![]() 的式子表示);
的式子表示);
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内有2014条直线a1,a2,…,a2014,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,依此类推,那么a1与a2014的位置关系是( )
A. 垂直
B. 平行
C. 垂直或平行
D. 重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种药品原价为36元/盒,经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.36(1﹣x)2=36﹣25
B.36(1﹣2x)=25
C.36(1﹣x)2=25
D.36(1﹣x2)=25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市按以下规定收取每月的水费:用水不超过10立方米,按每立方米2.1元收费;如果超过10立方米,超过部分按每立方米3元收费,已知某用户l2月水费平均每立方米2.5元.
按要求回答下列问题:
(1)这个用户12月用水量10立方米(填“超过”或“不超过”).
(2)在(1)的前提下,求12月这个用户的用水量是多少立方米?
(3)该用户12月份需交水费元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4![]() a,连接KB并延长交抛物线于点Q,求PQ的长.
a,连接KB并延长交抛物线于点Q,求PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com