解:(1)设客车由高速公路从甲地到乙地需x小时,则走普通公路需2x小时,
根据题意得:
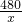
=
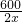
+45,
解得x=4,
经检验,x=4原方程的根,
答:客车由高速公路从甲地到乙地需4小时;
(2)①根据题意及所列的方程可知被墨水污染的部分为:甲、乙两队合作4天;
②设规定的工期为x天,
根据题意列出方程:
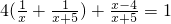
,
解得:x=20.
经检验:x=20是原分式方程的解.
这三种施工方案需要的工程款分别为:
(A)1.5×20=30(万元);
(B)1.1×(20+5)=27.5(万元);
(C)1.5×4+1.1×20=28(万元).
∵27.5<28<30,
∴施工方案B最节省工程款;
③由于方案B不能如期完工,根据②中的计算,若我是工程领导小组的组长,为了节省工程款,同时又能如期完工,将选择C方案:即由甲、乙两队合作4天,剩下的工程由乙队独做.
故答案为:甲、乙两队合作4天;B.
分析:(1)设客车由高速公路从甲地到乙地需x小时,则根据“由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半”可知走普通公路需2x小时,根据“客车在高速公路上行驶的平均速度比在普通公路上快45km/h”,得出等量关系:客车在高速公路上行驶的平均速度=在普通公路上行驶的平均速度+45,据此列出方程,解方程检验即可;
(2)①设规定的工期为x天,根据题意得出的方程为:
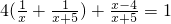
,知被墨水污染的部分为:甲、乙两队合作4天;
②根据题意先求得规定的天数,然后算出三种方案的价钱之后,再根据题意进行选择;
③根据(2)中计算的结果可得答案.
点评:本题主要考查分式方程的应用,找到关键描述语,找到合适的等量关系是解决问题的关键.

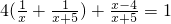
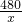 =
=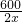 +45,
+45,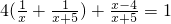 ,
,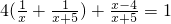 ,知被墨水污染的部分为:甲、乙两队合作4天;
,知被墨水污染的部分为:甲、乙两队合作4天;
