
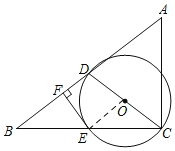
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O交BC于点E,过点E作EF⊥AB于点F.
(1)判断EF所在直线与⊙O的位置关系,并说明理由.
(2)若∠B=40°,⊙O的半径为6,求![]() 的长.(结果保留π)
的长.(结果保留π)

【答案】(1)EF与⊙O相切,理由见解析;(2)![]()
【解析】
(1)如图,连接OE,根据直角三角形的性质得到CD=BD,得到∠DBC=∠DCB,根据等腰三角形的性质得到∠OEC=∠OCE,得到∠OEC=∠DBC,推出∠OEF=90°,于是得到结论;
(2)根据弧长公式计算.
(1)EF所在直线与⊙O相切.
如图,连结OE.
∵∠ACB=90°,D为AB的中点,
∴BD=CD.
∴∠B=∠DCB.
∵OE=OC,
∴∠OEC=∠OCE.
∴∠OEC=∠B.
∴OE∥DB.
∴∠OEF=∠BFE.
∵EF⊥AB,
∴∠BFE=90°.
∴∠OEF=90°.
∵点E在⊙O上,∴EF与⊙O相切.
(2)∵∠OCE+∠OEC+∠EOC=180°,
∠OCE=∠OEC=∠B=40°,
∴∠EOC=180°﹣∠OCE﹣∠OEC=180°﹣40°﹣40°=100°.
∴![]() 的长
的长![]() .
.


科目:初中数学 来源: 题型:
【题目】某企业为响应国家教育扶贫的号召,决定对某乡镇全体贫困初、高中学生进行资助,初中学生每月资助200元,高中学生每月资助300元.已知该乡受资助的初中学生人数是受资助的高中学生人数的2倍,且该企业在2018年下半年7﹣12月这6个月资助学生共支出10.5万元.
(1)问该乡镇分别有多少名初中学生和高中学生获得了资助?
(2)2018年7﹣12月期间,受资助的初、高中学生中,分别有30%和40%的学生被评为优秀学生,从而获得了该乡镇政府的公开表扬.同时,提供资助的企业为了激发更多受资助学生的进取心和学习热情,决定对2019年上半年1﹣6月被评为优秀学生的初中学生每人每月增加a%的资助,对被评为优秀学生的高中学生每人每月增加2a%的资助.在此奖励政策的鼓励下,2019年1﹣6月被评为优秀学生的初、高中学生分別比2018年7﹣12月的人数增加了3a%、a%.这样,2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
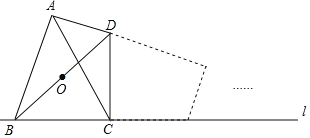
【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,AC平分∠BAD,AC=7,AD=3![]() ,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
,将四边形ABCD沿直线l无滑动翻滚一周,则对角线BD的中点O经过的路径长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于A(﹣2,0),点B(4,0).

(1)求抛物线的解析式;
(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;
(3)在直线的上方,抛物线是否存在点M,使四边形ABMC的面积为15?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场计划用96米的竹篱笆围成如图所示的①、②、③三个养殖区域,其中区域①是正方形,区域②和③是矩形,且AG∶BG=3∶2.设BG的长为2x米.
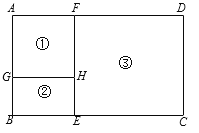
(1)用含x的代数式表示DF= ;
(2)x为何值时,区域③的面积为180平方米;
(3)x为何值时,区域③的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,动点
点运动,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,如果
点运动,如果![]() ,
,![]() 两点同时出发,当
两点同时出发,当![]() 到达
到达![]() 点处时,两点都停止运动.设运动的时间为
点处时,两点都停止运动.设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() .
.
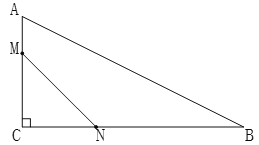
(1)用含![]() 的代数式表示:
的代数式表示:
![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
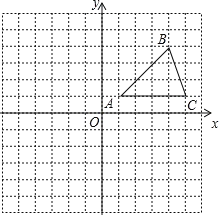
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
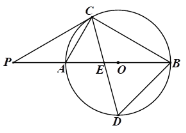
【题目】如图,△ABC内接于⊙O,AB为直径,∠BAC=60°,延长BA至点P使AP=AC, 作CD平分∠ACB交AB于点E,交⊙O于点D. 连结PC,BD.
(1)求证:PC为⊙O的切线;
(2)求证:BD=![]() PA;
PA;
(3)若PC=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com