
【题目】请阅读下列解题过程:
解一元二次不等式:x2-3x>0.
解:x(x-3)>0,
∴![]() 或
或![]() ,
,
解得x>3或x<0.
∴一元二次不等式x2-3x>0的解集为x<0或x>3.
结合上述解题过程回答下列问题:
(1)上述解题过程渗透的数学思想为 ;
(2)一元二次不等式x2-3x<0的解集为 ;
(3)请用类似的方法解一元二次不等式:x2-2x-3<0.
【答案】(1)转化的思想;(2)0<x<3;(3)-1<x<3
【解析】
(1)阅读解题过程知,解题过程渗透的数学思想为转化的思想;
(2)利用提公因式法进行因式分解,从而转化为两个一元一次不等式组求解即可;
(2)利用“十字相乘法”对不等式的左边进行因式分解,从而转化为两个一元一次不等式组求解即可.
(1)根据解题过程知,解题过程渗透的数学思想为:转化的思想;
(2)∵x2-3x<0,即x(x-3)<0,
∴![]() 或
或![]() ,
,
解得:0<x<3,
∴一元二次不等式x2-3x<0的解集为0<x<3;
(3)x2-2x-3<0,即(x-3)(x+1)<0,
则![]() 或
或![]() ,
,
解得:-1<x<3.
∴一元二次不等式x2-2x-3<0的解集为:-1<x<3.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】有这样一道习题:如图1,已知OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,过Q点作⊙O的切线交OA的延长线于R.
(1)证明:RP=RQ;
(2)请探究下列变化:
A、变化一:交换题设与结论.已知:如图1,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点(不与O、A重合),BP的延长线交⊙O于Q,R是OA的延长线上一点,且RP=RQ.证明:RQ为⊙O的切线.

B、变化二:运动探求. ①如图2,若OA向上平移,变化一中结论还成立吗?(只交待判断) 答:_________.
②如图3,如果P在OA的延长线上时,BP交⊙O于Q,过点Q作⊙O的切线交OA的延长线于R,原题中的结论还成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )
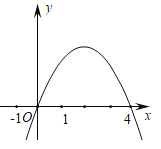
A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角些标系中,二次函数y=ax2+bx﹣![]() 的图象经过点A(﹣1,0),C(2,0),与y轴交于点B,其对称轴与x轴交于点D.
的图象经过点A(﹣1,0),C(2,0),与y轴交于点B,其对称轴与x轴交于点D.
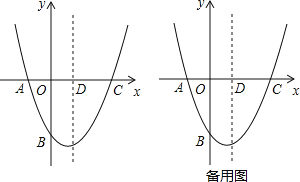
(1)求二次函数的表达式及其顶点的坐标;
(2)若P为y轴上的一个动点,连接PD,求![]() PB+PD的最小值;
PB+PD的最小值;
(3)M(x,t)为抛物线对称轴上一个动点,若平面内存在点N,使得以A、B、M、N为顶点的四边形为菱形,则这样的点N共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
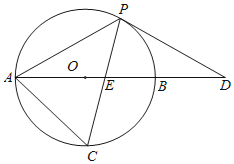
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=2,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论:
①∠BOD=90°;②DO∥AB;③CD=AD;④△BDE∽△BCD;⑤![]()
正确的有( )
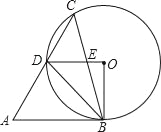
A. ①② B. ①④⑤ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
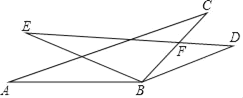
【题目】如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.
求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC( )
即∠ABC=∠EBD
在△ABC和△EBD中,
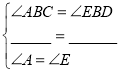 ,
,
∴△ABC≌△EBD( ),
∴∠C=∠D( )
∵∠FBD=∠D,
∴∠C= (等量代换),
∴AC∥BD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
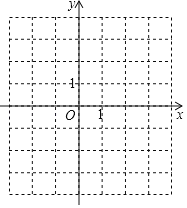
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
(1)求二次函数的解析式;
(2)在图中,画出二次函数的图象;
(3)根据图象,直接写出当y≤0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
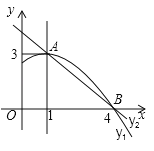
【题目】如图是抛物线![]() 图像的一部分,抛物线的项点坐标是A(1,3),与
图像的一部分,抛物线的项点坐标是A(1,3),与![]() 轴的一个交点B(4,0),直线
轴的一个交点B(4,0),直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,下列结论:①
两点,下列结论:①![]() :②
:②![]()
![]() ;③方程
;③方程![]() 有两个相等的实数根:④当
有两个相等的实数根:④当![]() 时,有
时,有![]() ;⑤抛物线与
;⑤抛物线与![]() 轴的另一个交点是(-1,0),其中正确的是( )
轴的另一个交点是(-1,0),其中正确的是( )
A.①②③B.①③④C.①③⑤D.②④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com