
【题目】抛物线y=x2+bx+c与直线y=﹣3x交于点A,点A横坐标为n﹣1,其中n>1,将OA绕点O逆时针旋转90°后形成OB,点B恰好在抛物线上.
(1)求抛物线的解析式(用含n的代数式表示);
(2)若抛物线与直线y=﹣x+2n﹣5交于C,D两点,且CD=2![]() ,则m值为多少?
,则m值为多少?
(3)若n为整数,当在x轴下方的抛物线上恰好有5个整数点(横坐标为整数),求出n值.
【答案】(1)y=x2﹣(4n﹣6)x+3n2﹣11n+8;(2)n=![]() ;(3)n=﹣1,﹣2,﹣3或3或4.
;(3)n=﹣1,﹣2,﹣3或3或4.
【解析】
(1)点A在直线y=-3x,则点A(n-1,-3n+3),将OA绕点O逆时针旋转90°后形成OB,由旋转的性质得点B(3n-3,n-1),即可求解;
(2)过D点作x轴的垂线,与过C点作y轴的垂线交于E点,则xC-xD=![]() CD=2,则
CD=2,则![]() ,则
,则![]() ,即可求解;
,即可求解;
(3)抛物线在x轴下方恰好有5个整数点,则4<|x1-x2|<6,则16<(|x1-x2|)2<36,即可求解.
(1)由题意得点A在直线y=﹣3x,且A点横坐标为n-1,
∴点A(n﹣1,﹣3n+3),
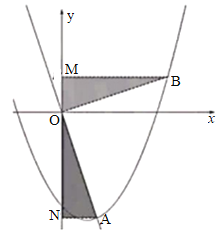
过A,B两点分别向y轴作垂线,垂足分别为N、M,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
∴B点坐标为(3n-3,n-1),
将A,B两点代入抛物线解析式求得:y=x2﹣(4n﹣6)x+3n2﹣11n+8;
(2)过D点作x轴的垂线,与过C点作y轴的垂线交于E点,
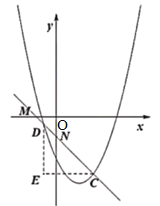
已知直线y=﹣x+2n﹣5交x轴于M(2n-5,0),交y轴于点N(0,2n-5),
![]() ,
,![]() ,
,![]() ,
,
∵CD=2![]() ,
,
∴![]() ,
,
∵直线与抛物线相交,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
解得,![]() (舍去)
(舍去)
∴n=![]()
(3)令y=0,则y=x2﹣(4n﹣6)x+3n2﹣11n+8=0,
则x1+x2=4n﹣6,x1x2=3n2﹣11n+8,
∵抛物线在x轴下方恰好有5个整数点,
∴4<|x1﹣x2|<6,则16<(|x1﹣x2|)2<36,
(|x1﹣x2|)2=(x1+x2)2﹣4x1x2=4n2﹣4n+4,
∴3<n2﹣n<18,
![]() <n<
<n<![]() 或
或![]() <n<
<n<![]()
∵n为整数,
故n=﹣1,﹣2,﹣3或3或4.


科目:初中数学 来源: 题型:
【题目】悬索桥,又名吊桥,指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁. 其缆索几何形状一般近似于抛物线.从缆索垂下许多吊杆(吊杆垂直于桥面),把桥面吊住.某悬索桥(如图1),是连接两个地区的重要通道. 图2是该悬索桥的示意图.小明在游览该大桥时,被这座雄伟壮观的大桥所吸引. 他通过查找资料了解到此桥的相关信息:这座桥的缆索(即图2中桥上方的曲线)的形状近似于抛物线,两端的索塔在桥面以上部分高度相同,即AB=CD, 两个索塔均与桥面垂直. 主桥AC的长为600 m,引桥CE的长为124 m.缆索最低处的吊杆MN长为3 m,桥面上与点M相距100 m处的吊杆PQ长为13 m.若将缆索的形状视为抛物线,请你根据小明获得的信息,建立适当的平面直角坐标系,求出索塔顶端D与锚点E的距离.


图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图, ![]() 是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是
是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是![]() ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间
,当点P到达点B时,P、Q两点停止运动,设点P的运动时间![]() ,解答下列各问题:
,解答下列各问题:
![]() 经过
经过![]() 秒时,求
秒时,求![]() 的面积;
的面积;
![]() 当t为何值时,
当t为何值时, ![]() 是直角三角形?
是直角三角形?
![]() 是否存在某一时刻t,使四边形APQC的面积是
是否存在某一时刻t,使四边形APQC的面积是![]() 面积的三分之二?如果存在,求出t的值;不存在请说明理由.
面积的三分之二?如果存在,求出t的值;不存在请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠C = 90°,AD是∠BAC的角平分线.
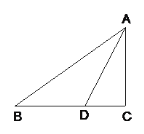
(1)请尺规作图:作⊙O,使圆心O在AB上,且A点在圆⊙O上.![]() (不写作法,保留作图痕迹);
(不写作法,保留作图痕迹);
(2)判断直线BC与所作⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
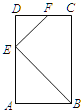
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于点F.
(1)求证:△ABE∽△DEF;
(2)求CF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学5次数学选拔赛的成绩统计如下表,他们5次考试的总成绩相同,请同学们完成下列问题:
第1 次 | 第2 次 | 第 3次 | 第 4次 | 第5 次 | |
甲成绩 | 90 | 40 | 70 | 40 | 60 |
乙成绩 | 70 | 50 | 70 |
| 70 |
(1)统计表中,求![]() 的值,甲同学成绩的极差为多少;
的值,甲同学成绩的极差为多少;
(2)小颖计算了甲同学的成绩平均数为60,方差是![]() [(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
[(90﹣60)2+(40﹣60)2+(70﹣60)2+(40﹣60)2+(60﹣60)2]=360.
请你求出乙同学成绩的平均数和方差;
(3)从平均数和方差的角度分析,甲乙两位同学谁的成绩更稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
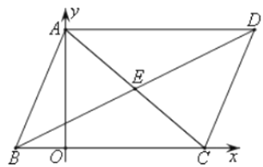
【题目】如图,在平面直角坐标系中,平行四边形ABCD中顶点A坐标(0,6),顶点B坐标(-2,0),顶点C坐标(8,0),点E为平行四边形ABCD的对角线的交点,求过点E且到点C的距离最大的直线解析式____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com