
【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

【答案】(1)∠C=60°.
(2)∠C-∠B=2∠DEF.理由见解析
【解析】试题分析:(1)已知:EF⊥BC,∠DEF=10°可以求得∠EDF的度数,∠EDF又是ABD的外角,已知∠B的度数,可求得∠BAD的值,AD平分∠BAC,所以∠BAC的值也可求出,从而求出∠C。(2)EF⊥BC,可得到∠EDF=90°-∠DEF,∠EDF又是ABD的外角,可得到∠BAD=∠EDF-∠B=90°-∠DEF-∠B,然后可将![]() BAC用含∠DEF、∠B的角来表示,即
BAC用含∠DEF、∠B的角来表示,即![]() BAC =2(90°-∠DEF-∠B),最后利用∠B、
BAC =2(90°-∠DEF-∠B),最后利用∠B、![]() BAC、
BAC、![]() C的和为180°求得三角之间的等量关系。
C的和为180°求得三角之间的等量关系。
试题解析:(1)∵EF⊥BC,∠DEF=10°,
∴∠EDF=80°.
∵∠B=40°,
∴∠BAD=∠EDF-∠B=80°-40°=40°.
∵AD平分∠BAC,∴∠BAC=80°.
∴∠C=180°-40°-80°=60°.
(2)∠C-∠B=2∠DEF.理由如下:
∵EF⊥BC,∴∠EDF=90°-∠DEF.
∵∠EDF=∠B+∠BAD,
∴∠BAD=90°-∠DEF-∠B.
∵AD平分∠BAC,
∴∠BAC=2∠BAD=180°-2∠DEF-2∠B.
∴∠B+180°-2∠DEF-2∠B+∠C=180°.
∴∠C-∠B=2∠DEF.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】在下列各数![]() 中,负数的个数为m个,正数的个数为n个,绝对值最大的数为k.
中,负数的个数为m个,正数的个数为n个,绝对值最大的数为k.
(1)m= __________.n=__________.K=__________.
(2)求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在下列横线上用含有![]() 的代数式表示相应图形的面积.
的代数式表示相应图形的面积.

① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表达: .
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于点
于点![]() .
.
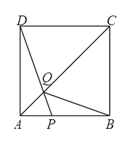
(![]() )试证明:无论点
)试证明:无论点![]() 运动到
运动到![]() 上何处时,都有
上何处时,都有![]() ≌
≌![]() .
.
(![]() )若点
)若点![]() 从点
从点![]() 运动到点
运动到点![]() ,再继续在
,再继续在![]() 上运动到点
上运动到点![]() ,在整个运动过程中,当点
,在整个运动过程中,当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 恰为等腰三角形.
恰为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2.
![]()
(1)A、B对应的数分别为 、 ;
(2)点A、B分别以4个单位/秒和3个单位/秒的速度相向而行,则几秒后A、B相距1个单位长度?
(3)点A、B以(2)中的速度同时向右运动,点P从原点O以7个单位/秒的速度向右运动,是否存在常数m,使得![]() 为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.
为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已引起社会各界的高度关注,有关部门在全国范围内对![]() 岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
岁的网瘾人群进行了简单的随机抽样调查,得到了如图所示的两个不完全统计图.
请根据图中的信息,解决下列问题:
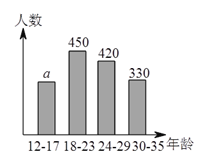
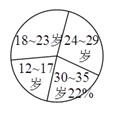
(![]() )求条形统计图中
)求条形统计图中![]() 的值.
的值.
(![]() )求扇形统计图中
)求扇形统计图中![]() 岁部分所占的百分比;
岁部分所占的百分比;
(![]() )据报道,目前我国
)据报道,目前我国![]() 岁网瘾人数约为
岁网瘾人数约为![]() 万,请估计其中
万,请估计其中![]() 岁的人数.
岁的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
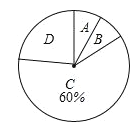
【题目】(2016山东潍坊第20题)今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com