已知:抛物线y=ax2+4ax+t与x轴的一个交点为A(-1,0)
(1)求抛物线与x轴的另一个交点B的坐标;
(2)D是抛物线与y轴的交点,C是抛物线上的一点,且以AB为一底的梯形ABCD的面积为9,求此抛物线的解析式;
(3)E是第二象限内到x轴、y轴的距离的比为5:2的点,如果点E在(2)中的抛物线上,且它与点A在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点P,使△APE的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)根据抛物线的解析式可知:抛物线的对称轴为x=-2,由此可求出B点的坐标.
(2)可将A点坐标代入抛物线的解析式中,求出a与t的关系式,然后将抛物线中的t用a替换掉,根据这个抛物线的解析式可表示出C点的坐标,然后根据梯形的面积求出a的值,即可得出抛物线的解析式.
(3)可根据E点横坐标与纵坐标的比例关系以及所处的象限设出E点的坐标,然后将它代入抛物线的解析式中即可求出E点的坐标.要使PA+EP最小,根据轴对称图象的性质和两点间线段最短可知:如果去A关于抛物线对称轴的对称点B,连接BE,那么BE与抛物线对称轴的交点就是P点的位置,可先求出直线BE的解析式然后联立抛物线的对称轴方程即可求出P的坐标.
解答: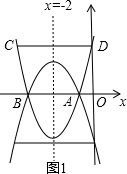
解:(1)依题意,抛物线的对称轴为x=-2,
∵抛物线与x轴的一个交点为A(-1,0),
∴由抛物线的对称性,可得抛物线与x轴的另一个交点B的坐标为(-3,0).
(2)∵抛物线y=ax
2+4ax+t与x轴的一个交点为A(-1,0)
∴a(-1)
2+4a(-1)+t=0
∴t=3a
∴y=ax
2+4ax+3a
∴D(0,3a)
∴梯形ABCD中,AB∥CD,且点C在抛物线y=ax
2+4ax+3a上,
∵C(-4,3a)
∴AB=2,CD=4
∵梯形ABCD的面积为9
∴
(AB+CD)•OD=9
∴
(2+4)•|3a|=9
∴a=±1
∴所求抛物线的解析式为y=x
2+4x+3或y=-x
2-4x-3.
(3)设点E坐标为(x
0,y
0),
依题意,x
0<0,y
0>0,且
=∴y
0=-
x
0①设点E在抛物线y=x
2+4x+3上,
∴y
0=x
02+4x
0+3
解方程组
得
,
∵点E与点A在对称轴x=-2的同侧
∴点E坐标为(
-,
).
设在抛物线的对称轴x=-2上存在一点P,使△APE的周长最小.
∵AE长为定值,
∴要使△APE的周长最小,只须PA+PE最小
∴点A关于对称轴x=-2的对称点是B(-3,0)
∴由几何知识可知,P是直线BE与对称轴x=-2的交点
设过点E、B的直线的解析式为y=mx+n
∴
,
解得
∴直线BE的解析式为y=
x+
∴把x=-2代入上式,得y=
∴点P坐标为(-2,
)
②设点E在抛物线y=-x
2-4x-3上
∴y
0=-x
02-4x
0-3,
解方程组
消去y
0,得
+x0+3=0∴△<0
∴此方程组无实数根.
综上,在抛物线的对称轴上存在点P(-2,
),使△APE的周长最小.
点评:本题主要考查了二次函数解析式的确定、图象面积的求法等知识点.综合性强,难度较大.

 解:(1)依题意,抛物线的对称轴为x=-2,
解:(1)依题意,抛物线的对称轴为x=-2,


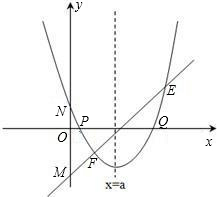 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
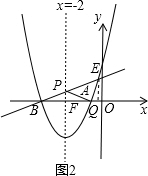
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. (2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.
(2013•贵阳)已知:直线y=ax+b过抛物线y=-x2-2x+3的顶点P,如图所示.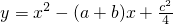 ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否
,抛物线与x轴交于点P、Q,问是否 存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由. ,其中a、b、c是△ABC的∠A、∠B、∠C的对边.
,其中a、b、c是△ABC的∠A、∠B、∠C的对边. ,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.
,抛物线与x轴交于点P、Q,问是否存在过P、Q两点且与y轴相切的圆?若存在,求出圆的圆心坐标,若不存在,请说明理由.