
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
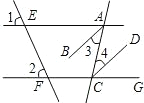
 如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整. | 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年浙江平阳苏步青学校八年级上学期期中数学试卷(带解析) 题型:解答题
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:∵ ∠1=∠2 ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴ ∠ =  ∠EAC,∠4=
∠EAC,∠4=  ∠ ( 角平分线的定义 )
∠ ( 角平分线的定义 )
∴ ∠ =∠4(等量代换)
∴ AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省八里店一中七年级第二学期期中考试数学试卷(带解析) 题型:解答题
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.
证明:∵ ∠1="∠2" ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴∠ = ∠EAC,∠4=
∠EAC,∠4= ∠ ( 角平分线的定义 )
∠ ( 角平分线的定义 )
∴∠ =∠4(等量代换)
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源:2012届浙江平阳苏步青学校八年级上学期期中数学试卷(解析版) 题型:解答题
如图,直线AE、CF分别被直线EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.将下列证明AB∥CD的过程及理由填写完整.

证明:∵ ∠1=∠2 ( 已知 )
∴ AE∥ ( )
∴ ∠EAC =∠ ,( )
而AB平分∠EAC,CD平分∠ACG( 已知 )
∴ ∠ =  ∠EAC,∠4=
∠EAC,∠4=  ∠
( 角平分线的定义 )
∠
( 角平分线的定义 )
∴ ∠ =∠4(等量代换)
∴ AB∥CD( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com