
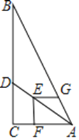
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G.若EF = EG,则CD的长为______.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果品超市销售进价为40元/箱的苹果,市场调查发现,若以每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱,设每箱苹果的销售价为x(元)(x>50)时,平均每天的销售利润为w(元).
(1)求w与x之间的函数关系式;
(2)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润为多少元?
(3)临近春节,为稳定市场,物价部门规定每箱苹果售价不得高于58元,求此时平均每天获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用放大镜看△ABC,若边BC的长度变为原来的2倍,那么下列说法中,不正确的是( ).
A.边AB的长度也变为原来的2倍;B.∠BAC的度数也变为原来的2倍;
C.△ABC的周长变为原来的2倍;D.△ABC的面积变为原来的4倍;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形ABCD中,E,F分别是边AB,AD上的点,过点F作EF的垂线交DC于点H,以EF为直径作半圆O.
(1)填空:点A (填“在”或“不在”)⊙O上;当弦AE等于弦AF时,![]() 的值是 ;
的值是 ;
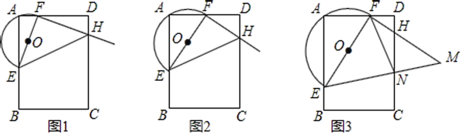
(2)如图1,在△EFH中,当FE=FH时,求证:AD=AE+DH;
(3)如图2,当△EFH的顶点F是边AD的中点时,求证:EH=AE+DH;
(4)如图3,点M在线段FH的延长线上,若FM=FE,连接EM交DC于点N,连接FN,当AE=AD时,FN=4,HN=3,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
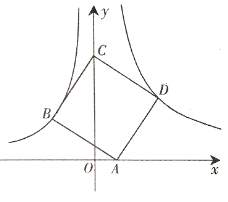
【题目】如图,正方形 ABCD 的顶点 A 在 x 轴的正半轴上,顶点 C 在 y 轴的正半轴上,点 B 在双曲线 y ![]() ( x 0) 上,点 D 在双曲线 y
( x 0) 上,点 D 在双曲线 y ![]() ( x 0) 上,点 D 的坐标是 (3,3).
( x 0) 上,点 D 的坐标是 (3,3).
(1)求 k 的值
(2)求点 A 和点 C 的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AC=BC,∠ACB=α,点D是平面内不与点A和点B重合的一点,连接DB,将线段DB绕点D顺时针旋转α得到线段DE,连接AE、BE、CD.
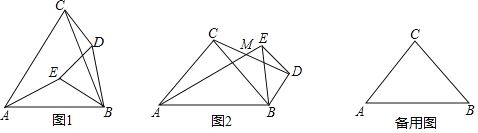
(1)如图①,点D与点A在直线BC的两侧,α=60°时,![]() 的值是 ;直线AE与直线CD相交所成的锐角的度数是 度;
的值是 ;直线AE与直线CD相交所成的锐角的度数是 度;
(2)如图②,点D与点A在直线BC两侧,α=90°时,求![]() 的值及直线AE与直线CD相交所成的锐角∠AMC的度数;
的值及直线AE与直线CD相交所成的锐角∠AMC的度数;
(3)当α=90°,点D在直线AB的上方,S△ABD=![]() S△ABC,请直接写出当点C、D、E在同一直线上时,
S△ABC,请直接写出当点C、D、E在同一直线上时,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的一个动点,作
上的一个动点,作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,射线
,射线![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
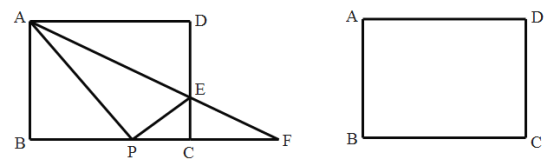
(1)如图,当![]() 在边
在边![]() 上时(点
上时(点![]() 与点
与点![]() 、
、![]() 都不重合),求
都不重合),求![]() 关于
关于![]() 的函数解析式,并写出它的定义域;
的函数解析式,并写出它的定义域;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com