
【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )
A.65°
B.66°
C.70°
D.78°
【答案】C
【解析】解:∵∠ABC、∠ACB的三等分线交于点E、D,
∴∠FBC=2∠DBC,∠GCB=2∠DCB,
∵∠BFC=132°,∠BGC=118°,
∴∠FBC+∠DCB=180°-∠BFC=180°-132°=48°,
∠DBC+∠GCB=180°-∠BGC=180°-118°=62°,
则
|
由①+②可得:3(∠DBC+∠DCB)=110°,
∴∠ABC+∠ACB=3(∠DBC+∠DCB)=110°,
∴∠A=180°-(∠ABC+∠ACB)=180°-110°=70°,
故选C.
【考点精析】本题主要考查了三角形的内角和外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.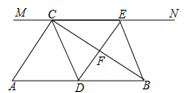
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A(m,y1),B(m﹣2,y2)两点都在该函数的图象上,当m=时,y1=y2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点P(m,m﹣n)与点Q(2,3)关于原点对称,则点M(m,n)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
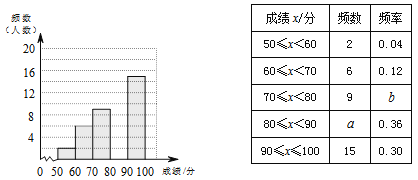
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC, ∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=118°,则∠A的度数为( )
A.65°
B.66°
C.70°
D.78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为斜边AB的中点.
(1)如图1,当点P与点Q重合时,AE与BF的位置关系,QE与QF的数量关系.
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.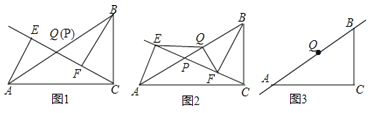
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com