
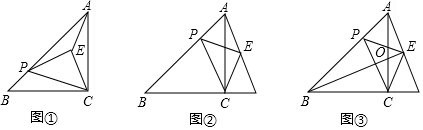
分析 (1)∠先求出APC=67.5°,再根据三角形的内角和得出∠ACP=67.5°=∠APC,即AP=AC进而判断出在△PAE≌△CAE,即可得出∠PAE=∠CAE,即可;
(2)先判断出∠PFC=∠PAC,即可得出A,P,C,F四点共圆,即∠CAF=∠CPF=45°,最后用同角或等角的余角相等即可得出结论;
(3)先判断出∠AEO=∠ACD=90°,进而判断出△AOE∽△ADC,即可得出$\frac{OE}{AE}=\frac{CD}{AC}$代值化简即可得出结论.
解答 解:(1)在△ABC中,∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵∠APC=∠B+∠BPC=45°+22.5°=67.5°,
∴∠ACP=180°-∠BAC-∠APC=67.5°=∠APC,
∴AP=AC,
∵△PCE是等腰直角三角形,
∴∠EPC=∠ECP,
∴∠APE=∠ACE,
在△PAE和△CAE中,$\left\{\begin{array}{l}{PE=AC}\\{∠APE=∠ACE}\\{PE=CE}\end{array}\right.$,
∴△PAE≌△CAE,
∴∠PAE=∠CAE,
∴AE平分∠BAC;
(2)如图③,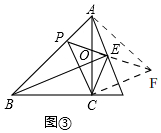
延长PE至F,使EF=PE,延长AF,CF,
∴∠PFC=45°,
∵∠PAC=45°,
∴∠PFC=∠PAC,
∴A,P,C,F四点共圆,
∴∠CAF=∠CPF=45°,
∴∠PAF=45°+45°=90°,
∵PE=EF,
∴AE=PE,
∵PE=CE,
∴AE=CE,
∴∠CAD=∠ACE,
∵∠CAE+∠D=90°,∠ACE+∠ECD=90°,
∴∠ECD=∠D,
∴CE=DE,∴AE=DE,
(3)在△ABD中,∵BE是∠ABC的平分线,
∴∠ABE=∠DBE,AE=BE,
∴BE⊥AD,
∴∠AEO=∠ACD=90°,
∵∠CAD=∠CAD,
∴△AOE∽△ADC,
∴$\frac{OE}{AE}=\frac{CD}{AC}$,
∵AC=($\sqrt{2}$+1)CD,
∴$\frac{OE}{AE}=\sqrt{2}-1$,
∵AE=CE,
∴$\frac{OE}{CE}=\sqrt{2}-1$,
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,角平分线的定义,作出辅助线是解本题的关键,是一道比较好的中考常考题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,下列判断正确的是:( )
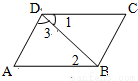
A. 若∠1=∠2,则AD∥BC B. 若∠1=∠2,则AB∥CD
C. 若∠A=∠3,则AD∥BC D. 若∠3+∠DAB=180° ,则AB∥CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com