
【题目】已知: ![]() ,
,![]() .
.
(1)当x=1和-1时,分别求P,Q的值;
(2)当x=19时,P的值为a, Q的值为b,当x=-19时,分别求P, Q的值(用含a,b的代数式表示);
(3)当x=m时,P, Q的值分别为c, d; 当x=-m时,P, Q的值分别为e, f,则在c,d, e, f四个有理数中,以下判断正确的是 (只要填序号即可).
①有两个相等的正数;②有两个互为相反数;③至多有两个正数;④至少有两个正数;⑤至多有一个负数;⑥至少有一个负数.
【答案】(1)当x=1时,P=9,Q=12;当x=-1时,P=-9,Q=12;(2)P=-a,Q=b;(3)①②④⑤.
【解析】
(1)分别代入求值即可;
(2)根据互为相反数的两个数的奇次幂仍然互为相反数,互为相反数的两个数的偶次幂相等可得答案;
(3)首先求出c,d,e,f并化简,然后利用相反数的和偶次方的性质逐个判断即可.
解:(1)当x=1时,![]() ,
,![]() ;
;
当x=-1时,![]() ,
,![]() ;
;
(2)∵当x=19时,P的值为a,Q的值为b,
∴当x=-19时,P=-a,Q=b;
(3)由题意得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
①∵![]() ,∴
,∴![]() ,即有两个相等的正数,正确;
,即有两个相等的正数,正确;
②∵![]() ,
,![]() ,∴有两个互为相反数,正确;
,∴有两个互为相反数,正确;
③∵![]() ,ce互为相反数,∴至少有两个正数,错误;
,ce互为相反数,∴至少有两个正数,错误;
④由③可知,正确;
⑤∵![]() ,ce互为相反数,∴至多有一个负数,正确;
,ce互为相反数,∴至多有一个负数,正确;
⑥由⑤可知,错误;
故判断正确的是:①②④⑤.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
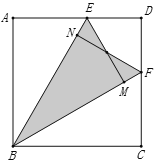
【题目】如图,正方形ABCD的边长为![]() ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
③连接FC.
(2)猜想与证明:猜想四边形ABCF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若a+b=2,则称a与b是关于1的平衡数.
(1)直接填写:①3与_ 是关于1的平衡数: :
②1-x与________是关于 1的平衡数(用含x的代数式表示);
(2)若![]() ,
,![]() ,先化简a. b,再判断a与b是否是关于1的平衡数.
,先化简a. b,再判断a与b是否是关于1的平衡数.
查看答案和解析>>
科目:初中数学 来源: 题型:
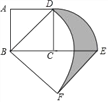
【题目】如图,正方形ABCD中,AB=2,将线段CD绕点C顺时针旋转90°得到线段CE,线段BD绕点B顺时针旋转90°得到线段BF,连接BF,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
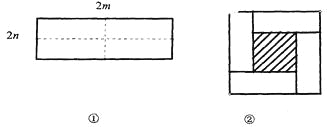
(1)你认为图②中的阴影部分的正方形的边长等于_________________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①_________________________________________________________.
方法②_________________________________________________________.
(3)观察图②,你能写出![]() ,
,![]() ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,……滿足下列条件:a1=0,a2=-│a1+1│,a3=-│a2+2│,a4=-│a3+3│,·……,依次类推,则a2017的值为 ( )
A.-1007B.-1008C.-1009D.-2016
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com