
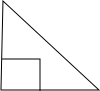
 如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )
如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )| A. | 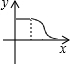 | B. |  | C. |  | D. | 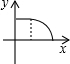 |
分析 这是一个分段函数,当0≤x≤1时,重叠部分的面积y为正方形的面积;当1<x≤2时,重叠部分的面积为五边形的面积;当2<x≤3时,重叠部分的面积是三角形的面积,根据等腰直角三角形的面积公式列出函数关系式.
解答 解: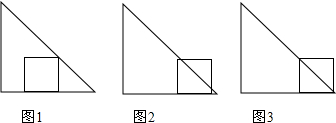
如图1,当0≤x≤1时,y=1×1=1,即y=1.
如图2,当1<x≤2时,y=-$\frac{1}{2}$(x-1)2+1,图象是开口向下的抛物线.
如图3,当2<x≤3时,y=$\frac{1}{2}$(3-x)2=$\frac{1}{2}$(x-3)2,图象是开口向上的抛物线.
故选:A.
点评 本题考查了动点问题的函数图象.函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.


科目:初中数学 来源: 题型:选择题
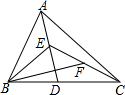 在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
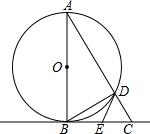 如图,AB是⊙O的直径,BC是⊙O的切线,弦AD的延长线交直线BC与点C,
如图,AB是⊙O的直径,BC是⊙O的切线,弦AD的延长线交直线BC与点C,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
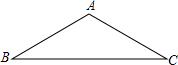 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com