
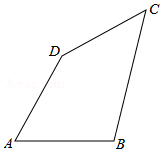
 如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.
如图,在四边形ABCD中,AB=AD=8,∠A=60°,BC=10,CD=6.分析 (1)连接BD,根据AB=AD=8,∠A=60°,得出△ABD是等边三角形,求得BD=8,然后根据勾股定理的逆定理判断三角形BDC是直角三角形,从而求得∠ADC=150°;
(2)根据四边形的面积等于三角形ABD和三角形BCD的和即可求得.
解答 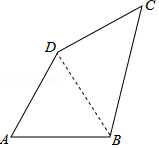 解:(1)连接BD,
解:(1)连接BD,
∵AB=AD=8,∠A=60°,
∴△ABD是等边三角形,
∴BD=8,∠ADB=60°,
∵BC=10,CD=6,
则BD2+CD2=82+62=100,BC2=102=100,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=150°;
(2)S=S△ABD+S△BDC
=$\frac{1}{2}$AD•$\frac{\sqrt{3}}{2}$AD+$\frac{1}{2}$BD•DC
=$\frac{1}{2}$×8×$\frac{\sqrt{3}}{2}$×8+$\frac{1}{2}$×8×6
=16$\sqrt{3}$+24.
点评 本题考查了等边三角形的判定和性质,直角三角形的判定和性质,把不规则的图形转化成规则的三角形求得面积等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.
如图,在△ABC中,∠B=90°,AB=$\sqrt{3}$,将AC沿AE折叠,使点C与点D重合,且DE⊥BC,则AE=$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
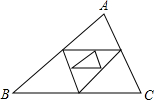 如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )
如图,△ABC周长为1,连接△ABC三边中点构成第二个三角形,再连接第二个三角形三边中点构成第三个三角形,以此类推,第2016个三角形的周长为( )| A. | 22016 | B. | 22017 | C. | ${(\frac{1}{2})}^{2016}$ | D. | ${(\frac{1}{2})}^{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
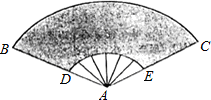 如图,扇形纸扇完全打开后,阴影部分为贴纸,外侧两竹条AB,AC的夹角为120°,弧BC的长为30πcm,AD的长为15cm,则贴纸的面积等于600πcm2.
如图,扇形纸扇完全打开后,阴影部分为贴纸,外侧两竹条AB,AC的夹角为120°,弧BC的长为30πcm,AD的长为15cm,则贴纸的面积等于600πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com