
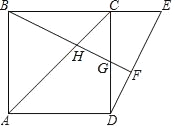
【题目】如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.
(1)求证:GDAB=DFBG;
(2)联结CF,求证:∠CFB=45°.
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)先证明△BGC∽△DGF,然后根据相似三角形的性质列比例式整理即可;(2)连接BD、CF,由△BGC∽△DGF,可得![]() ,变形得
,变形得![]() ,可证△BGD∽△CGF,从而∠BDG=∠CFG,再根据正方形的性质求出∠BDG即可.
,可证△BGD∽△CGF,从而∠BDG=∠CFG,再根据正方形的性质求出∠BDG即可.
证明:(1)∵四边形ABCD是正方形
∴∠BCD=∠ADC=90°,AB=BC,
∵BF⊥DE,
∴∠GFD=90°,
∴∠BCD=∠GFD,
∵∠BGC=∠FGD,
∴△BGC∽△DGF,
∴![]() ,
,
∴DGBC=DFBG,
∵AB=BC,
∴DGAB=DFBG;
(2)如图,连接BD、CF,

∵△BGC∽△DGF,
∴![]() ,
,
∴![]() ,
,
又∵∠BGD=∠CGF,
∴△BGD∽△CGF,
∴∠BDG=∠CFG,
∵四边形ABCD是正方形,BD是对角线,
∴![]() ,
,
∴∠CFG=45°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
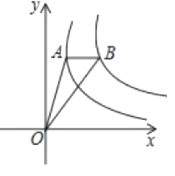
【题目】如图,点A是反比例函数y![]() =
=![]() (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y![]() =
=![]() (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明父子晨起锻炼身体,两人同时从家出发,小明跑步的速度为每分钟200米,爸爸跑步速度是150米,出发后15分钟后,小明到达广场,立即以一定的速度按原路线返回,3分钟后与爸爸相遇,爸爸与小明仍按小明返回时的速度返回家,下面的图象反应的是父子两人离家的距离与离家时间的关系,观察图回答问题;
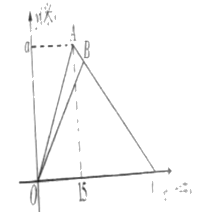
(1)图中a=________________,图中B的坐标为_________________;
(2)求返回时直线AC的解析式:
(3)求运动过程中父子两人何时相距250米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为治理污水,甲乙两区都需要各自铺设一段污水排放管道。甲乙两区八月份都各铺了![]() 米,在九月份和十月份中,甲区的工作量平均每月增长
米,在九月份和十月份中,甲区的工作量平均每月增长![]() ,乙区则平均每月减少
,乙区则平均每月减少![]() 。
。
(1)九月份甲铺设了____________米排污管,乙铺设了_____________米排污管;(用含字母![]() 的代数式表示)
的代数式表示)
(2)如果![]() 且
且![]() ,那么十月份甲区比乙区多铺多少米排污管?
,那么十月份甲区比乙区多铺多少米排污管?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由
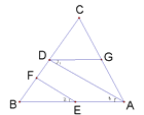
如图:EF∥AD,∠1=∠2,∠BAC=70°,把求∠AGD的过程填写完整.
证明:∵EF∥AD
∴∠2= ( )
又∵∠1=∠2
∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
又∵∠BAC=70°
∴∠AGD=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
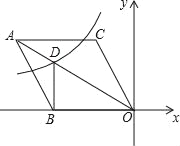
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3![]() ),反比例函数y=
),反比例函数y=![]() 的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是_____.
的图象与菱形对角线AO交于点D,连接BD,当BD⊥x轴时,k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com