
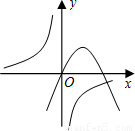
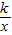 ,y=kx2-
,y=kx2-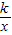 ,y=kx2+
,y=kx2+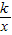 ,y=kx2+
,y=kx2+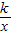 ,y=-kx2-
,y=-kx2- 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 (2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表:
(2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13种植某数y | 6 | 8 | 10 | 12 | 14 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| 63 |
| 65 |
| 66 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
1.求反比例函数与二次函数的解析式;
2.设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
3.若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
1.求反比例函数与二次函数的解析式;
2.设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
3.若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积
查看答案和解析>>
科目:初中数学 来源:2011年北京房山区九年级学题统一练习(二) 题型:解答题
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
1.求反比例函数与二次函数的解析式;
2.设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
3.若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积
查看答案和解析>>
科目:初中数学 来源:2011年北京房山区九年级学题统一练习(二) 题型:解答题
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点A(2,2)
1.求反比例函数与二次函数的解析式;
2.设二次函数图象的顶点为B,判断点B是否在反比例函数的图象上,并说明理由;
3.若反比例函数图象上有一点P,点P的横坐标为1,求△AOP的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com