
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 2 |
| 10 |
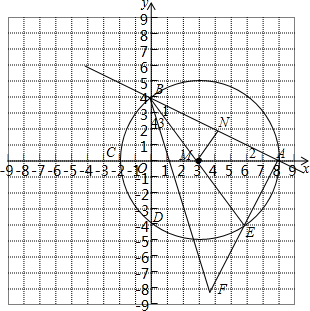 解:(1)作MN⊥AB于N,如图,
解:(1)作MN⊥AB于N,如图,| 1 |
| 2 |
| OB2+OA2 |
| 5 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
| 2 |
| 2 |
| 5 |
| 10 |


科目:初中数学 来源: 题型:
 我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一,为了增强居民的节水意识,某自来水公司对居民用水采取以户为单位分段计费办法收费:即每月用水10吨以内(包括10吨)的用户,每吨水收费a元,每月用水超过10吨的部分,按每吨b元(b>a)收费,设一户居民月用水x(吨),应收水费y(元),y与x之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
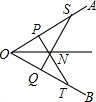 如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.
如图,在∠AOB的OA边上取两点P和S,再在OB上取两点Q和T,使OP=OQ,OT=OS,PT=QS,PT与QS相交于点N,求证:ON平分∠AOB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com