
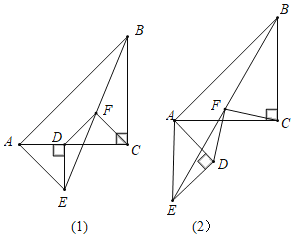
【题目】已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.
(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45度时,若AD=DE=2,AB=6,求此时线段CF的长.
【答案】(1)DF=CF,DF⊥CF,(2)![]() .
.
【解析】
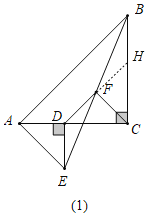
(1)如图1,延长DF交BC于H,由“AAS”可证△DEF≌△HBF,可得DF=FH,DE=BH,可证DC=CH,由等腰直角三角形的性质可得DF=CF,DF⊥CF;
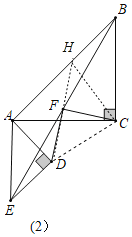
(2)延长DF交BA于点H,连接CH,CD,由“AAS”可证△DEF≌△HBF,可得DF=FH,DE=BH,由“SAS”可证△ADC≌△BHC,可得CH=CD,∠ACD=∠BCH,由由勾股定理和等腰直角三角形的性质可求CF的长.
解:(1)DF=CF,DF⊥CF,
理由如下:如图1,延长DF交BC于H,
∵点F为BE中点,
∴BF=EF,
∵△ABC和△ADE都是等腰直角三角形,
∴AD=ED,AC=BC,∠ACB=∠ADE=∠CDE=90°,
∴BC∥DE,
∴∠BHF=∠EDF,且BF=EF,∠DFE=∠BFH,
∴△DEF≌△HBF(AAS)
∴DF=FH,DE=BH,
∵AD=ED=BH,AC=BC
∴DC=CH,且DF=FH,∠ACB=90°,
∴CF=DF,CF⊥DF;
(2)如图2,延长DF交BA于点H,连接CH,CD,
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠ABC=45°,
∵由旋转可以得出,∠CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,且∠DEF=∠HBF,∠EFD=∠BFH,
∴△DEF≌△HBF(AAS),
∴ED=HB=2,DF=FH,
∵AB=6,
∴AH=4
在Rt△HAD中,DH=![]()
∵AD=BH=DE,AC=BC,∠DAC=∠ABC=45°,
∴△ADC≌△BHC(SAS)
∴CH=CD,∠ACD=∠BCH,
∵∠BCH+∠ACH=90°,
∴∠ACD+∠ACH=90°,
∴∠DCH=90°,且CH=CD,DF=FH,
∴CF=DF=FH=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
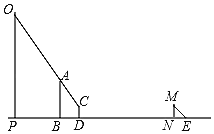
【题目】如图,笑笑和爸爸想要测量直立在地面上的建筑物OP与广告牌AB的高度.首先,笑笑站在离广告牌B处4米的D处看到广告牌AB的顶端A、建筑物OP的顶端O一条直线上;此时,在阳光下,爸爸站在N处,他的影长NE=2.1米,同一时刻,测得建筑物OP的影长为PG=28米,已知建筑物OP与广告牌AB之间的水平距离为11米,笑笑的眼睛到地面的距离CD=1.5米,爸爸的身高MN=1.8米.
(1)请你画出表示建筑物OP在阳光下的影子PG;
(2)求:①建筑物OP的高度;
②广告牌AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
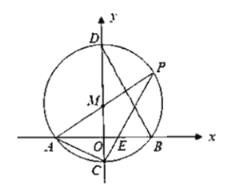
【题目】如图,在平面直角坐标系中,以点![]() 为圆心,作
为圆心,作![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 、
、![]() 两点,连结
两点,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,连结
,连结![]() 交
交![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)求弦![]() 的长;
的长;
(2)求直线![]() 的函数解析式;
的函数解析式;
(3)连结![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.
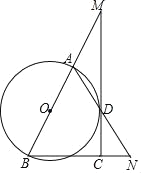
(1)求证:AB=BN;
(2)若MD=4,CD=2.4,求![]() 。
。
(3)若AM=2,CN=1.2,求⊙O的半径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
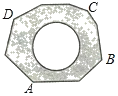
【题目】如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为2米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
掷小石子落在不规则图形内的总次数 | 50 | 150 | 300 | … |
小石子落在圆内(含圆上)的次数m | 20 | 59 | 123 | … |
小石子落在圆外的阴影部分(含外缘)的次数n | 29 | 91 | 176 | … |
(1)当投掷的次数很大时,则m:n的值越来越接近 (结果精确到0.1)
(2)若以小石子所落的有效区域为总数(即m+n),则随着投掷次数的增大,小石子落在圆内(含圆上)的频率值稳定在 附近(结果精确到0.1);
(3)请你利用(2)中所得频率的值,估计整个封闭图形ABCD的面积是多少平方米?(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
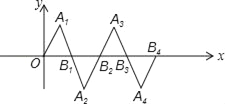
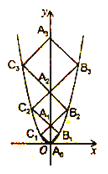
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
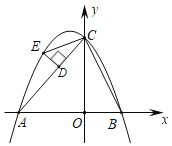
【题目】如图,已知抛物线与坐标轴交于A(﹣4,0)、B(2,0)、C(0,4),连接BC,AC.
(1)求抛物线的解析式;
(2)若点E是抛物线在第二象限上的一点,过点E作DE⊥AC于点D,求DE的最大值.
(3)若点E是抛物线上第二象限上的一动点,过点E作DE⊥AC于点D,连接CE,若△CDE与△COB相似,直接写出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲乙两地同时销售某种品牌的汽车,已知在甲地的总销售利润y(单位:万元)与销售量x(单位:辆)之间满足y=﹣![]() x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
(1)求W与x的函数关系式;
(2)甲乙两地各销售多少辆车时W最大?W的最大值是多少?
(3)为了开拓甲地市场,公司规定甲地平均每辆汽车的销售利润不高于2万元,那么公司销售这30辆汽车可获得的最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图,点
的图象如图,点![]() 位于坐标原点,点
位于坐标原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在二次函数位于第一象限的图象上,点
在二次函数位于第一象限的图象上,点![]() 在二次函数位于第二象限的图象上,四边形
在二次函数位于第二象限的图象上,四边形![]() ,四边形
,四边形![]() ,四边形
,四边形![]() …四边形
…四边形![]() 都是正方形,则正方形
都是正方形,则正方形![]() 的周长为__________.
的周长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com