
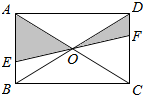
 如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,如果矩形的面积为1,那么阴影部分的面积是$\frac{1}{4}$.
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,如果矩形的面积为1,那么阴影部分的面积是$\frac{1}{4}$. 分析 本题主要根据矩形的性质,得△EBO≌△FDO,推出阴影部分的面积=S△AEO+S△EBO=S△AOB=$\frac{1}{4}$S矩形ABCD.
解答 解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
$\left\{\begin{array}{l}{∠EOB=∠DOF}\\{OB=OD}\\{∠EBO=∠FDO}\end{array}\right.$,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=S△AEO+S△EBO=S△AOB=$\frac{1}{4}$S矩形ABCD=$\frac{1}{4}$,
故答案为$\frac{1}{4}$.
点评 本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com