
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,若点P从点A出发,以每秒2cm的速度沿折线A-C-B-A运动,设运动时间为t秒(t>0).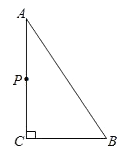
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求t的值;
(3)在运动过程中,直接写出当t为何值时,△BCP为等腰三角形.
【答案】
(1)解:设存在点P,使得PA=PB,
此时PA=PB=2t,PC=4-2t,
在Rt△PCB中,PC2+CB2=PB2,
即:(4-2t)2+32=(2t)2,
解得:t= ![]() ,
,
∴当t= ![]() 时,PA=PB
时,PA=PB
(2)解:当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,
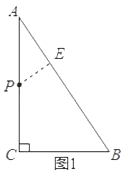
此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,
在Rt△BEP中,PE2+BE2=BP2,
即:(2t-4)2+12=(7-2t)2,
解得:t= ![]() ,
,
∴当t= ![]() 时,P在△ABC的角平分线上
时,P在△ABC的角平分线上
(3)解:在Rt△ABC中,∵AB=5cm,BC=3cm,
∴AC=4cm,
根据题意得:AP=2t,
当P在AC上时,△BCP为等腰三角形,
∴PC=BC,即4-2t=3,
∴t= ![]() ,
,
当P在AB上时,△BCP为等腰三角形,
①CP=PB,点P在BC的垂直平分线上,
如图2,过P作PE⊥BC于E,
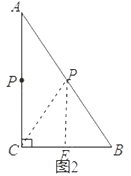
∴BE= ![]() BC=
BC= ![]() ,
,
∴PB= ![]() AB,即2t-3-4=
AB,即2t-3-4= ![]() ,解得:t=
,解得:t= ![]() ,
,
②PB=BC,即2t-3-4=3,
解得:t=5,
③PC=BC,如图3,过C作CF⊥AB于F,

∴BF= ![]() BP,
BP,
∵∠ACB=90°,
由射影定理得;BC2=BFAB,
即33= ![]() ×5,
×5,
解得:t= ![]() ,
,
∴当t= ![]() ,5,
,5, ![]() ,
, ![]() 时,△BCP为等腰三角形.
时,△BCP为等腰三角形.
【解析】(1)设存在点P,使得PA=PB,此时PA=PB=2t,PC=4-2t,根据勾股定理列方程即可得到结论;
(2)当点P在∠CAB的平分线上时,如图1,过点P作PE⊥AB于点E,此时BP=7-2t,PE=PC=2t-4,BE=5-4=1,根据勾股定理列方程即可得到结论;
(3)在Rt△ABC中,根据勾股定理得到AC=4cm,根据题意得:AP=2t,当P在AC上时,△BCP为等腰三角形,得到PC=BC,即4-2t=3,求得t的值,,当P在AB上时,△BCP为等腰三角形,①CP=PB,点P在BC的垂直平分线上,如图2,过P作PE⊥BC于E,求得t的值,②PB=BC,即2t-3-4=3,解得t的值,③PC=BC,如图3,过C作CF⊥AB于F,由射影定理得;BC2=BFAB,列出方程求解即可得出结论。


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
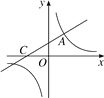
【题目】如图,直线y=![]() x+2与双曲线y=
x+2与双曲线y=![]() 相交于点A(m,3),与x轴交于点C.
相交于点A(m,3),与x轴交于点C.
(1)求双曲线的解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(4,8),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为 . 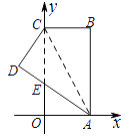
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(3)班体训队员的身高(单位:cm)如下:169,165,166,164,169,167,166,169,166,165,获得这组数据方法是( )
A.直接观察
B.查阅文献资料
C.互联网查询
D.测量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com