
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
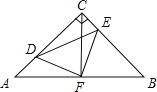
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.
(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.
证明:(1)在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中,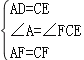 ,
,
∴△ADF≌△CEF(SAS);
(2)由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
A. ①②③④ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平整的地面上,有若干个完全相同棱长的小正方体堆成一个几何体,如图所示.
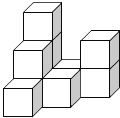
(1)请画出这个几何体的三视图.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色.
(3)若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一块长80mm、宽60mm的铁皮的4个角分别剪去一个边长相等的小正方形,做成一个底面积是1500mm2的无盖铁盒。若设小正方形的边长为xmm,下面所列的方程中,正确的是( )
A.(80-x)(60-x)=1500
B.(80-2x)(60-2x)=1500
C.(80-2x)(60-x)=1500
D.(80-x)(60-2x)=1500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,正确的有( )
(1)相等的圆心角所对的弧相等;
(2)平分弦的直径垂直于弦;
(3)长度相等的两条弧是等弧
(4) 圆是轴对称图形,任何一条直径都是对称轴
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.

(1)求该抛物线的解析式;
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
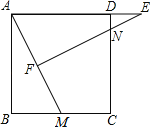
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com