
【题目】阅读理解:
我们知道:一条线段有两个端点,线段![]() 和线段
和线段![]() 表示同一条线段. 若在直线
表示同一条线段. 若在直线![]() 上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了
上取了三个不同的点,则以它们为端点的线段共有 条;若取了四个不同的点,则共有线段 条;…;依此类推,取了![]() 个不同的点,共有线段条.(用含
个不同的点,共有线段条.(用含![]() 的代数式表示)
的代数式表示)
类比探究:
以一个锐角的顶点为端点向这个角的内部引射线.
(1)若引出两条射线,则所得图形中共有 个锐角;
(2)若引出![]() 条射线,则所得图形中共有 个锐角.(用含
条射线,则所得图形中共有 个锐角.(用含![]() 的代数式表示)
的代数式表示)
拓展应用:
一条铁路上共有8个火车站,若一列火车往返过程中必须停靠每个车站,则铁路局需为这条线路准备多少种车票?
【答案】![]() ; (1)6; (2)
; (1)6; (2) ![]() ; 拓展应用: 铁路局需为这条线路准备56种车票.
; 拓展应用: 铁路局需为这条线路准备56种车票.
【解析】
对于“阅读理解”,假如l上取三点A,B,C,则线段有AB,AC,BC,自己试着总结出规律,再根据线段的定义解答;
类比探究:根据角的定义解答;
拓展应用:先计算出线段的条数,再根据两站之间需要两种车票解答.
解答:
阅读理三个不同的点,以它们为端点的线段共有3条,
若取了四个不同的点,则共有线段6条,…,
依此类推,取了n个不同的点,共有线段n(n1)2条;
类比探究:
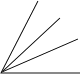
(1)引出两条射线,共有4条射线,锐角的个数为6;
(2)引出n条射线,共有n+2条射线,锐角的个数:![]() ;
;
拓展应用:8个火车站共有线段条数![]() =28,
=28,
需要车票的种数:28×2=56.
故答案为:3,6,![]() ;6;
;6;![]() ;56.
;56.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E. 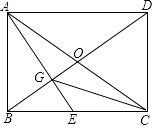
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴被折成![]() ,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。
,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字_________重合。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数图象的对称轴为直线x=2,顶点为点C,直线y=x+m与该二次函数的图象交于点A,B两点,其中点A的坐标为(5,8),点B在y轴上.
(1)求m的值和该二次函数的表达式.P为线段AB上一个动点(点P不与A,B两点重合),过点P作x轴的垂线,与这个二次函数的图象交于点E.
①设线段PE的长为h,求h与x之间的函数关系式,并写出自变量x的取值范围.
②若直线AB与这个二次函数图象的对称轴的交点为D,求当四边形DCEP是平行四边形时点P的坐标.
(2)若点P(x,y)为直线AB上的一个动点,试探究:以PB为直径的圆能否与坐标轴相切?如果能请求出点P的坐标,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
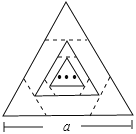
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣ ![]() x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N. 
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com