
【题目】如图,在△ABC中,∠BAC=90°,点O在BC上,以线段OC的长为半径的⊙O与AB相切于点D,分别交BC、AC于点E、F,连接ED并延长,交CA的延长线于点G.
(1)求证:∠DOC=2∠G.
(2)已知⊙O的半径为3.
①若BE=2,则DA= .
②当BE= 时,四边形DOCF为菱形.

【答案】(1)见解析;(2)①![]() ;②3.
;②3.
【解析】
(1)根据切线的性质可得∠ODB=90°,再根据平行线的判定可得OD∥CG,进而得到∠G=∠ODE,因为OD=OE,所以∠OED=∠ODE,最好根据圆周角为圆心角的一半即可得证;
(2)①利用勾股定理求得BD=4,由(1)知,OD∥CG,可得△BOD∽△BCA,再根据相似三角形的的性质求解即可;
②如图,连接DF,OF,根据菱形的性质可得DF=CF=OC=OD=3,进而可得△ODF为等边三角形,即∠ODF=60°,根据30°角所对直角边为斜边的一半可得AF=![]() ,进而可得AC=
,进而可得AC=![]() ,由(2)知△BOD∽△BCA,再根据相似三角形的的性质求解即可.
,由(2)知△BOD∽△BCA,再根据相似三角形的的性质求解即可.
(1)证明:∵AB为⊙O的切线,
∴OD⊥AB,
∴∠ODB=90°,
∴∠BAC=∠ODB=90°,
∴OD∥CG,
∴∠G=∠ODE,
∵OD=OE,
∴∠OED=∠ODE,
∵∠DOC=∠ODE+∠OED,
∴∠DOC=2∠ODE=2∠G;
(2)解:①在Rt△BOD中,
OD=3,OB=OE+BE=5,
∴BD=![]() =4,
=4,
由(1)知,OD∥CG,
∴△BOD∽△BCA,
∴![]() ,
,
即![]() ,
,
∴AD=![]() ,
,
故答案为:![]() ;
;
②如下图,连接DF,OF,
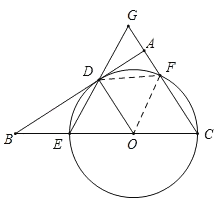
当四边形DOCF为菱形时,
DF=CF=OC=OD=3,
∵OF=3,
∴△ODF为等边三角形,
∴∠ODF=60°,
∴∠ADF=90°﹣∠ODF=30°,
在Rt△DAF中,DF=3,
∴AF=3×![]() =
=![]() ,
,
∴AC=CF+AF=![]() ,
,
由(2)知,∴△BOD∽△BCA,
∴![]() ,
,
即 ,
,
∴BE=3,
故答案为:3.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】小亮和小黄同学在实验室中调制体积相同但浓度不同的化学反应试剂![]() 溶液,已知小亮和小黄调制的
溶液,已知小亮和小黄调制的![]() 溶液浓度分别为
溶液浓度分别为![]() 、
、![]() .现将小亮调制的
.现将小亮调制的![]() 溶液的
溶液的![]() 倒入小黄调制的
倒入小黄调制的![]() 溶液中,混合均匀后再由小黄调制的
溶液中,混合均匀后再由小黄调制的![]() 溶液倒回小亮调制的
溶液倒回小亮调制的![]() 溶液使其体积恢复到原体积,则互掺后小亮、小黄调制的
溶液使其体积恢复到原体积,则互掺后小亮、小黄调制的![]() 溶液含纯
溶液含纯![]() 量的差与互掺前小亮、小黄调制的
量的差与互掺前小亮、小黄调制的![]() 溶液含纯
溶液含纯![]() 量的差之比为_______.
量的差之比为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为
的网格,网格中每个小正方形的边长均为![]() ,线段
,线段![]() 的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:
的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:

(1)在图1中画一个菱形![]() (非正方形),所画菱形各顶点必须在小正方形的顶点上;
(非正方形),所画菱形各顶点必须在小正方形的顶点上;
(2)在图2中画一个以线段![]() 为一边的等腰
为一边的等腰![]() ,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为
,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为边
为边![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),
不重合),![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,联结
,联结![]() 交对角线
交对角线![]() 于点
于点![]() .设
.设![]() ,
,![]() .
.

(1)求证:![]() 是等边三角形;
是等边三角形;
(2)求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)点![]() 是线段
是线段![]() 的中点,联结
的中点,联结![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
动手实践:数学课上老师让学生们折矩形纸片下面几幅图是学生们折出的一部分图形(沿直线![]() 折叠)由于折痕所在的直线不同,折出的图形也不同,各个图形中所“隐含的”基本图形也不同.我们可以通过发现基本图形研究这些图形中几何问题.
折叠)由于折痕所在的直线不同,折出的图形也不同,各个图形中所“隐含的”基本图形也不同.我们可以通过发现基本图形研究这些图形中几何问题.
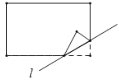
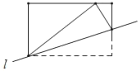
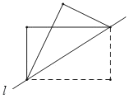
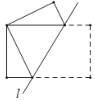
问题解决:(1)如图1,将矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 与点
与点![]() 重合,点
重合,点![]() 落在点
落在点![]() 的位置,连接
的位置,连接![]() ,
,![]() ,
,![]() ,线段
,线段![]() 交
交![]() 于点
于点![]() ,则
,则![]() 与
与![]() 的关系为 ,线段
的关系为 ,线段![]() 与线段
与线段![]() 的关系为 .
的关系为 .
小强量得![]() ,则
,则![]() .
.
小丽说:“四边形![]() 是菱形”,请你帮她证明.
是菱形”,请你帮她证明.
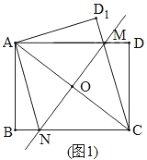
拓展延伸:(2)如图2,矩形纸片![]() 中,
中,![]() ,
,![]() ,小明将矩形纸片
,小明将矩形纸片![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 的位置,
的位置,![]() 交
交![]() 于点
于点![]() ,请你直接写出线段
,请你直接写出线段![]() 的长: .
的长: .
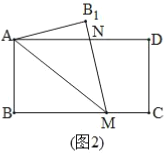
综合探究:(3)如图3,![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,
,![]() .在矩形
.在矩形![]() 的边
的边![]() 上取一点
上取一点![]() ,在
,在![]() 上取一点
上取一点![]() ,将纸片沿
,将纸片沿![]() 折叠,使线段
折叠,使线段![]() 与线段
与线段![]() 交于点
交于点![]() ,得到
,得到![]() .请你确定
.请你确定![]() 面积的取值范围 .
面积的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2交x轴于A(﹣1,0),B(4,0)两点,交y轴于点C,与过点C且平行于x轴的直线交于另一点D,点P是抛物线上一动点.
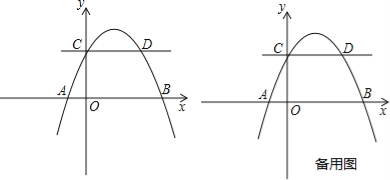
(1)求抛物线解析式及点D坐标;
(2)点E在x轴上,若以A,E,D,P为顶点的四边形是平行四边形,求此时点P的坐标;
(3)过点P作直线CD的垂线,垂足为Q,若将△CPQ沿CP翻折,点Q的对应点为Q′.是否存在点P,使Q′恰好落在x轴上?若存在,求出此时点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() :
:![]() (
(![]() ,
,![]() 是常数)经过
是常数)经过![]() 、
、![]() 两点.
两点.
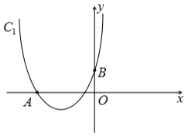
(1)求![]() ,
,![]() 的值;
的值;
(2)向右平移抛物线![]() ,使它经过点
,使它经过点![]() ,得抛物线
,得抛物线![]() ,
,![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,且在另一个交点的左侧.
,且在另一个交点的左侧.
①求抛物线![]() 的表达式;
的表达式;
②![]() 是点
是点![]() 关于抛物线
关于抛物线![]() 对称轴的对称点,
对称轴的对称点,![]() 是线段
是线段![]() 上一点,
上一点,![]() 轴,交抛物线
轴,交抛物线![]() 于点
于点![]() ,
,![]() 为垂足,设
为垂足,设![]() ,线段
,线段![]() 的长为
的长为![]() ,求
,求![]() 的值,使
的值,使![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级男生“跳绳”成绩的情况,随机选取该年级部分男生进行测试.以下是根据测试成绩绘制的统计图表的一部分.
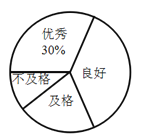
成绩等级 | 频数(人) | 频率 |
优秀 | ||
良好 | ||
及格 | 10 | 0.2 |
不及格 | 0.1 |
根据以上信息,解答下列问题:
(1)被测试男生中,成绩等级为“优秀”的男生人数占被测试男生总人数的百分比为________%,成绩等级为“及格”的男生人数为________人;
(2)被测试男生的总人数为________人,成绩等级为“不及格”的男生人数________人;
(3)若该校七年级共有570名男生,根据调查结果,估计该校七年级男生成绩等级为“良好”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com