
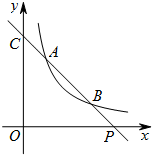
 如图,已知直线y=ax+b与双曲线$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.
如图,已知直线y=ax+b与双曲线$y=\frac{k}{x}$(x>0)交于A(x1,y1),B(x2,y2)两点(A与B不重合),直线AB与x轴交于P(x0,0),与y轴交于点C.分析 (1)把A点坐标代入反比例函数解析式可求得k,进一步可求得B点坐标,再利用待定系数法可求得直线解析式,可求得P点坐标;
(2)过点A作AD∥x轴,交x轴于点D,利用△ACD∽△PCO,结合A、P、C的坐标可求得x1、y1之间的关系,结合AB=BP可表示出B点坐标,再结合A、B两点都在反比例函数图象上,可求得A、B两点的坐标;
(3)结合(1)、(2)中的坐标可猜得结论.
解答 解:(1)∵点A(1,3)在反比例函数y=$\frac{k}{x}$上,
∴k=3,
∵点B(3,y2)在y=$\frac{3}{x}$上,
∴y2=1,即B点坐标为(3,1),
把A、B两点坐标代入直线y=ax+b,
可得$\left\{\begin{array}{l}{a+b=3}\\{3a+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为y=-x+4,
当y=0时,x=4,
∴P点坐标为(4,0);
(2)如图,过A作AD∥x轴,交y轴于点D,则AD⊥y轴,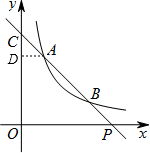
∴△ACD∽△PCO,
∴$\frac{CD}{OC}$=$\frac{AD}{OP}$,
∵b=y1+1,P(6,0),A(x1,y1),
∴CD=1,OC=y1+1,AD=x1,OP=6,
∴$\frac{1}{{y}_{1}+1}$=$\frac{{x}_{1}}{6}$,
∵AB=BP,A(x1,y1),
∴B为AP中点,且P为(6,0)
∴B点坐标为($\frac{{x}_{1}+6}{2}$,$\frac{{y}_{1}}{2}$),
∵A、B两点都在y=$\frac{k}{x}$上,
∴x1•y1=$\frac{{x}_{1}+6}{2}$•$\frac{{y}_{1}}{2}$,解得x1=2,
∴$\frac{1}{{y}_{1}+1}$=$\frac{2}{6}$,解得y1=2,
∴A(2,2),B(4,1);
(3)猜想x1,x2,x0之间的关系式为:x1+x2=x0.
理由如下:
∵A(x1,y1),B(x2,y2),
∴$\left\{\begin{array}{l}{a{x}_{1}+b={y}_{1}}\\{a{x}_{2}+b={y}_{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}}\\{b=-\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}-{x}_{1}}}\end{array}\right.$,
∴直线AB解析式为y=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$x-$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{x}_{2}-{x}_{1}}$,
令y=0可得x=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$,
∵x1y1=x2y2,
∴x=$\frac{{x}_{1}{y}_{2}-{x}_{2}{y}_{1}}{{y}_{2}-{y}_{1}}$=$\frac{({y}_{2}-{y}_{1})({x}_{1}+{x}_{2})}{{y}_{2}-{y}_{1}}$=x1+x2,
即x1+x2=x0.
点评 本题为反比例函数的综合应用,涉及知识点有待定系数法、相似三角形的判定和性质、中点坐标公式及方程思想等.在(1)中求得B点的坐标是解题的关键,在(2)中用A、P两点的坐标表示出P点的坐标是解题的关键,在(3)中观察(1)(2)的结论即可得到.本题考查知识点较多,综合性较强,难度适中.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
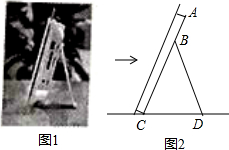 如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).
如图1是小红同学书桌上的一个电子相框,将其侧面抽象为如图2所示的几何图形,已知BC=BD=18cm,∠CBD=40°,则点B到CD的距离为16.9cm(用科学计算器计算.参考数据sin20°≈0.342,cos20°≈0.940,sin40°≈0.643,cos40°≈0.766,结果精确到0.1cm).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.114×1011 | B. | 1.14×1010 | C. | 11.4×109 | D. | 114×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
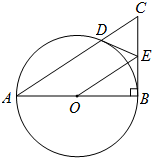 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
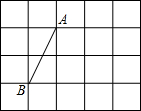 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 矩形一边长/m | 5 | 10 | 15 | 20 |
| 矩形面积/m2 | 125 | 200 | 225 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com