
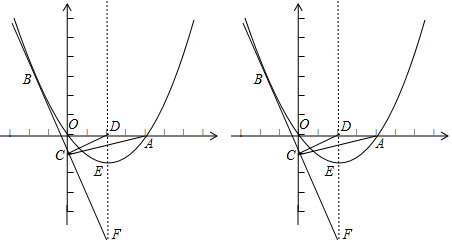
���� ��1�����������B�������m��ֵ��Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2����ADP���ADC�й�ͬ�ĵױ�AD����Ϊ�����ȣ�����AD���ϵĸ���ȣ���Ϊ1���Ӷ��õ���P��������Ϊ1�������������ߵĽ���ʽ�����P�������ꣻ
��3������ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�ע�ⲻҪ©�⣮���ÿһ�����Σ��ֱ���м��㣬����߶�MF�ij��ȣ��Ӷ��õ��˶�ʱ��t��ֵ��
��� �⣺��1���ߵ�B��-2��m����ֱ��y=-2x-1��
��m=-2����-2��-1=4-1=3��
���ԣ���B��-2��3����
�֡������߾���ԭ��O��
���������ߵĽ���ʽΪy=ax2+bx��
�ߵ�B��-2��3����A��4��0�����������ϣ�
��$\left\{\begin{array}{l}{4a-2b=3}\\{16a+4b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-1}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2-x��
��2����P��x��y�����������ϵ�һ�㣬
��P��x��$\frac{1}{4}$x2-x����
��S��ADP=S��ADC��
��S��ADC=$\frac{1}{2}$AD•OC��S��ADP=$\frac{1}{2}$AD•|y|��
�֡ߵ�C��ֱ��y=-2x-1��y�ύ�㣬
��C��0��-1����
��OC=1��
��|$\frac{1}{4}$x2-x|=1����$\frac{1}{4}$x2-x=1����$\frac{1}{4}$x2-x=-1��
��ã�x1=2+2$\sqrt{2}$��x2=2-2$\sqrt{2}$��x3=x4=2��
���P������Ϊ P1��2+2$\sqrt{2}$��1��P2=��2-2$\sqrt{2}$��1����P3��2��1����
��3�����ۣ����ڣ�
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2-x��
�ඥ��E��2��-1�����Գ���Ϊx=2��
��F��ֱ��y=-2x-1��Գ���x=2�Ľ��㣬��F��2��-5����DF=5��
�֡�A��4��0����
��AE=$\sqrt{5}$��
����ͼ��ʾ���ڵ�M���˶������У����γ����ĸ����Σ�
������AEM1Q1��
�ߴ�ʱEM1=AE=$\sqrt{5}$��
��M1F=DF-DE-DM1=4-$\sqrt{5}$��
��t1=4-$\sqrt{5}$��
������AEOM2��
�ߴ�ʱDM2=DE=1��
��M2F=DF+DM2=6��
��t2=6��
������AEM3Q3��
�ߴ�ʱEM3=AE=$\sqrt{5}$��
��DM3=EM3-DE=$\sqrt{5}$-1��
��M3F=DM3+DF=��$\sqrt{5}$-1��+5=4+$\sqrt{5}$��
��t3=4+$\sqrt{5}$��
������AM4EQ4��
��ʱAEΪ���εĶԽ��ߣ���Խ���AE��M4Q4���ڵ�H����AE��M4Q4��
����֪��AED�ס�M4EH��
��$\frac{{M}_{4}E}{AE}$=$\frac{EH}{DE}$����$\frac{{M}_{4}E}{\sqrt{5}}$=$\frac{\frac{\sqrt{5}}{2}}{1}$����M4E=$\frac{5}{2}$��
��DM4=M4E-DE=$\frac{5}{2}$-1=$\frac{3}{2}$��
��M4F=DM4+DF=$\frac{3}{2}$+5=$\frac{13}{2}$��
��t4=$\frac{13}{2}$��
�������������ڵ�M����Q��ʹ����Q��A��E��M�ĵ�Ϊ������ı��������Σ�ʱ��t��ֵΪ��t1=4-$\sqrt{5}$��t2=6��t3=4+$\sqrt{5}$��t4=$\frac{13}{2}$��
���� �����Ƕ��κ����ۺ��⣬�����֪ʶ��������κ�����ͼ�������ʡ�һ�κ���������ϵ������ͼ����������ε��ж������ʵȣ������漰�����ڶ࣬�����ѶȽϴڣ�2�����Ǵ��������⣬Ҫ�����������������ȹ�ϵ�����P�������꣬Ȼ�����÷���˼�����������ꣻ�ڣ�3�������˶������⣬ע������������������ĸ�������©�⣮


 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
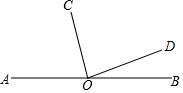 ��ͼ����O��ֱ��AB��һ�㣬OCƽ�֡�AOD�������BOD=30�㣬���AOC�Ķ�����
��ͼ����O��ֱ��AB��һ�㣬OCƽ�֡�AOD�������BOD=30�㣬���AOC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��1 | B�� | x��5 | C�� | -1��x��5 | D�� | -1��x��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ����·��˳����A��B��C���أ��ס�������ͬʱ��A�س������ֱ�����ǰ��B�ء�C�أ��׳�����B��ͣ��һ��ʱ���ԭ��ԭ·���أ��ҳ�����C�غ�����ԭ��ԭ·���أ��ҳ��ȼ׳���1Сʱ����A�أ��ס�������������ʻ��·��y��ǧ�ף���ʱ��x��ʱ��������������ʱ��ʼ��ʱ��֮��ĺ���ͼ����ͼ��ʾ��
��һ����·��˳����A��B��C���أ��ס�������ͬʱ��A�س������ֱ�����ǰ��B�ء�C�أ��׳�����B��ͣ��һ��ʱ���ԭ��ԭ·���أ��ҳ�����C�غ�����ԭ��ԭ·���أ��ҳ��ȼ׳���1Сʱ����A�أ��ס�������������ʻ��·��y��ǧ�ף���ʱ��x��ʱ��������������ʱ��ʼ��ʱ��֮��ĺ���ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
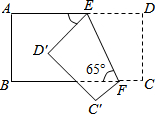 ��ͼ��ʾ����һ��������ֽƬ��EF�۵���D��C�ֱ�����D�䡢C���λ�ã�����EFB=65�㣬���C��FB���ڣ�������
��ͼ��ʾ����һ��������ֽƬ��EF�۵���D��C�ֱ�����D�䡢C���λ�ã�����EFB=65�㣬���C��FB���ڣ�������| A�� | 70�� | B�� | 65�� | C�� | 50�� | D�� | 25�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-4 | B�� | x2-2 | C�� | 4-x2 | D�� | x2+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
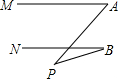 ��ͼ��ֱ��MA��NB����A=50�㣬��B=20�㣬���P=���������ȣ�
��ͼ��ֱ��MA��NB����A=50�㣬��B=20�㣬���P=���������ȣ�| A�� | 20 | B�� | 25 | C�� | 30 | D�� | 35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Ǹ���һ�������� | |
| B�� | ���������������������������� | |
| C�� | 0�Ȳ���������Ҳ���Ǹ��� | |
| D�� | ������������ֵͳ���������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com