D
分析:先判断出旋转6次所走过的路线正好是正六边形,然后用2012除以6,根据余数是2,停留在A
2处,然后过点作A
2B⊥A
0A
1于点B,然后求出A
1B、A
2B的长度,再根据点A
0的坐标是(1,0)解答即可.
解答:
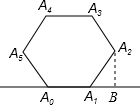
解:根据题意,每次都是逆时针旋转60°,
360°÷60°=6,
所以,旋转6次所走过的路线正好是正六边形,
∵2012÷6=335…2,
∴第2012次行走后与第2次行走到达的点相同,在点A
2处,
过点作A
2B⊥A
0A
1于点B,
∵每次前走2米,
∴A
1B=A
1A
2•cos60°=2×

=1,A
2B=A
1A
2•sin60°=2×

=

,
∵点A
0的坐标是(1,0),
∴点A
2的横坐标为1+2+1=4,
点A
2的坐标为(4,

),
即第2012次行走后的坐标是(4,

).
故选D.
点评:本题考查了坐标与图形的变化-旋转,根据题意判断出每旋转6次所走过的路线正好是正六边形,然后求出第2012次行走后的点与点A
2重合是解题的关键.

 )
) )
) )
) 解:根据题意,每次都是逆时针旋转60°,
解:根据题意,每次都是逆时针旋转60°, =1,A2B=A1A2•sin60°=2×
=1,A2B=A1A2•sin60°=2× =
= ,
, ),
), ).
).
