
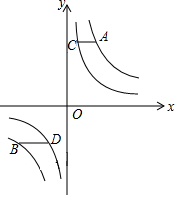
 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{12}{5}$ |
分析 设点A、C的纵坐标为y1,点B、D的纵坐标为y2,分别表示出来A、B、C、D四点的坐标,根据线段AC、BD的长度结合AC与BD间的距离,即可得出y1、y2的值,再由点A、B的横坐标结合AC=$\frac{4}{5}$即可求出m-n的值.
解答 解:设点A、C的纵坐标为y1,点B、D的纵坐标为y2,
则点A($\frac{m}{{y}_{1}}$,y1),点C($\frac{n}{{y}_{1}}$,y1),点B($\frac{m}{{y}_{2}}$,y2),点D($\frac{n}{{y}_{2}}$,y2).
∵AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,
∴$\frac{8}{5}$×|$\frac{m-n}{{y}_{1}}$|=|$\frac{m-n}{{y}_{2}}$|,
∴|y2|=$\frac{3}{5}$|y1|.
∵|y1|+|y2|=$\frac{24}{5}$,
∴y1=3,y2=-$\frac{9}{5}$.
∴AC=$\frac{m}{{y}_{1}}$-$\frac{n}{{y}_{1}}$=$\frac{m-n}{3}$=$\frac{4}{5}$,
∴a-b=$\frac{12}{5}$.
故选D.
点评 本题考查了两点间的距离、反比例函数图象上点的坐标特征以及反比例函数的性质,解题的关键是利用两点间的距离公式找出AB=$\frac{m-n}{3}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某批次圆珠笔的使用寿命 | |
| B. | 端午节期间,食品检查部门调查市场上粽子的质量情况 | |
| C. | 调查某班46同学的视力情况 | |
| D. | 检测我地区的空气质量 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
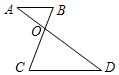 如图,已知AD、BC相交于点O,下列说法错误的是( )
如图,已知AD、BC相交于点O,下列说法错误的是( )| A. | 若AB∥CD,则∠B=∠C | B. | 若∠A=∠D,则AB∥CD | ||
| C. | 若∠B=∠AOB,则∠DOC=∠C | D. | ∠A+∠B=∠C+∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
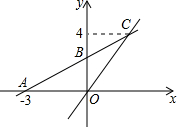 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交点为A(-3,0),与y轴交点为B,且与正比例函数y=$\frac{4}{3}x$的图象交于点C(m,4),求m的值及点B的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 样品 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 花朵的直径 (单位:cm) | 5 | 6 | 7 | 7 | 8 | 8 | 9 | 10 | 11 | 12 | 12 | 13 | 15 | 15 | 17 |
| 样品 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 花朵的直径 (单位:cm) | 7 | 8 | 8 | 9 | 9 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 12 | 13 | 15 |
| 优良品种数量 | 平均数 | |
| 甲试验田 | 8 | 10.33 |
| 乙试验田 | 8 | 10.33 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com