
| A. | 40% | B. | B56% | C. | 60% | D. | 62% |
分析 根据题意可得最大的三个数的和是6+7+7=20,再根据这五个数据的平均数是5,求出另外2个数的和,再写出五个学生投中的次数可能的一组数即可.
解答 解:∵中位数是6,唯一众数是7,
∴最大的三个数的和是:6+7+7=20,
∴另外2个数的和<10或另外2个数的和>0,
∴五个学生投中的次数的和<30或五个学生投中的次数的和>20,
∴他们投中次数占投篮总次数的百分率<$\frac{30}{50}$=60%或>$\frac{20}{50}$=40%,
∴他们投中次数占投篮总次数的百分率可能是56%,
故选B.
点评 此题考查了平均数、中位数和众数,一组数据中出现次数最多的数据叫做这组数据的众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数.


科目:初中数学 来源: 题型:填空题
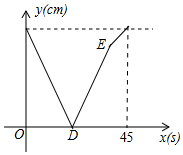 甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为y=4.5x-90(20≤x≤36).(并写出自变量取值范围)
甲、乙两动点分别从线段AB的两端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点A运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则图中线段DE所表示的函数关系式为y=4.5x-90(20≤x≤36).(并写出自变量取值范围)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com