
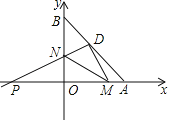
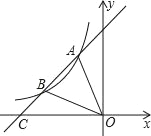
����Ŀ����ƽ��ֱ������ϵ�У���A�͵�B�ֱ���x����������y����������ϣ���OA=6��OB=8����D��AB���е㣮
��1��ֱ��д����D�����꼰AB�ij���
��2����ֱ�ǡ�NDM�Ƶ�D��ת������DP�ֱ�x�ᡢy���ڵ�P��N������DM��x���ڵ�M������MN��
�ٵ���P�͵�N�ֱ���x��ĸ������y���������ʱ������PDM�ס�MON�����N�����ꣻ
����ֱ�ǡ�NDM�Ƶ�D��ת�Ĺ����У���DMN�Ĵ�С�Ƿ�ᷢ���仯����˵�����ɣ�
���𰸡� ��1����D������Ϊ��3��4����AB=10����2���ٵ�N������Ϊ��0��![]() ��������ֱ�ǡ�NDM�Ƶ�D��ת�Ĺ����У���DMN�Ĵ�С���ᷢ���仯�����ɼ�����
��������ֱ�ǡ�NDM�Ƶ�D��ת�Ĺ����У���DMN�Ĵ�С���ᷢ���仯�����ɼ�����
��������
��1������OA��6��OB��8����D��AB���е㣬�ɵõ�D������Ϊ��3��4�������ݹ��ɶ����ɵ�AB![]() 10��
10��
��2�����ȹ���D��DC��y����C����DE��x����E����ó�CD��3��OE��DE��4��CO����DCN����DEM��90�㣬����ON��x����CN��4��x���ж���CDN�ס�EDM���ó�EM![]() ��4��x�����ж���CDN�ס�OPN���ó�OP
��4��x�����ж���CDN�ס�OPN���ó�OP![]() ���ٸ���PO��MO���ó�����x�ķ���
���ٸ���PO��MO���ó�����x�ķ���![]() ��4��x�������x��ֵ���ɵõ���N�����ꣻ
��4��x�������x��ֵ���ɵõ���N�����ꣻ
���ȸ��ݡ�CDN�ס�EDM���õ�![]() ���ٸ���OA��6��OB��8���õ�
���ٸ���OA��6��OB��8���õ�![]() ��������
��������![]() ����AOB����NDM��90�㣬�ж���AOB�ס�NDM���������������εĶ�Ӧ����ȣ��ɵá�DMN����OBA�������õ���DMN�Ĵ�С���ᷢ���仯��
����AOB����NDM��90�㣬�ж���AOB�ס�NDM���������������εĶ�Ӧ����ȣ��ɵá�DMN����OBA�������õ���DMN�Ĵ�С���ᷢ���仯��
��1����OA��6��OB��8����D��AB���е㣬���D������Ϊ��3��4����AB![]() 10��
10��
��2������ͼ������D��DC��y����C����DE��x����E����
CD��3��OE��DE��4��CO����DCN����DEM��90�㣬��ON��x����CN��4��x��
�ߡ�CDE����PDM��90�㣬���CDN����EDM�����CDN�ס�EDM����![]() ����
����![]() ����EM
����EM![]() ��4��x����
��4��x����
��CD��PO�����CDN�ס�OPN����![]() ����
����![]() ����OP
����OP![]() ��
��
�ߡ�PDM�ס�MON�����NPO����NMO����PN��MN��
��NO��PM����PO��MO����![]() ��4��x������ã�x1��10����ȥ����x2
��4��x������ã�x1��10����ȥ����x2![]() ����ON
����ON![]() �����N��������0��
�����N��������0��![]() ����
����
����ֱ�ǡ�NDM�Ƶ�D��ת�Ĺ����У���DMN�Ĵ�С���ᷢ���仯���������£�
�����ɵã���CDN�ס�EDM����![]() ����
����![]() ��
��
�֡�OA��6��OB��8����![]() ����
����![]() ����
����![]() ��
��
�֡ߡ�AOB����NDM��90�㣬���AOB�ס�NDM�����DMN����OBA��
�ߡ�OBA��С���䣬���DMN�Ĵ�С���ᷢ���仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC����AC��BC��2����P����б��ABΪֱ���İ�Բ����MΪPC���е㣮����P�ذ�Բ�ӵ�A�˶�����Bʱ����M�˶���·��������������

A. �� B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ĵ�����װ��4����ͬ��С�����dz���ɫ����������𣬰����Ƿֱ��ţ�1��2��3��4��
(1)�������һ��С��Żز�ҡ�ȣ����������һ�������б�����״ͼ�ķ������������ȡ��������ͬ���ĸ�����
(2)�����������С��ֱ��д��������ȡ�������ź�Ϊ�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AMNΪ���������Σ���O�ǵױ�MN���е㣬��AN���O�����ڵ�E��ON���O�ཻ�ڵ�D��
��1����֤��AM���O���У�
��2����EN=![]() ��DN=2������Ӱ���ֵ������
��DN=2������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
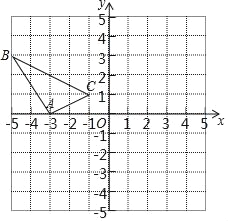
����Ŀ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У�������ͼ��ʾ��ƽ��ֱ������ϵ��ABC�Ǹ�������Σ������������ߵĽ����ϣ�
��1��������ABC����ԭ��O�����ĶԳƵ���A1B1C1���ٰ���A1B1C1����ƽ��4����λ���ȵõ���A2B2C2��
��2����A2B2C2����ABC�Ƿ����ij������ĶԳƣ����ǣ�ֱ��д���Գ����ĵ����ꣻ�����ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����E��BC�ߵ��е㣬DE��AC�ཻ�ڵ�F������BF�����н��ۣ���S��ABF=S��ADF��S��CDF=4S��CEF����S��ADF=2S��CEF����S��ADF=2S��CDF��������ȷ���ǣ�������
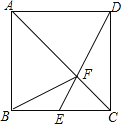
A. �٢� B. �ڢ� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
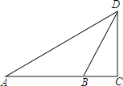
����Ŀ����ͼ���ڡ�ADC�У���C=90�㣬��A=30�㣮��B���߶�AC��һ�㣬��AB=40cm����DBC=75�㣮
��1�����B��AD�ľ��룻
��2�����߶�CD�ij�������ø��ű�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����
����![]() Ϊ���������ȱ�������
Ϊ���������ȱ�������![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() .���н��ۣ���
.���н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() .����ȷ�Ľ�����_____.(�����)
.����ȷ�Ľ�����_____.(�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx+b�뷴��������y��![]() ��x��0����ͼ���ཻ�ڵ�A����B����X�ύ�ڵ�C�����е�A����1��3���͵�B����3��n����
��x��0����ͼ���ཻ�ڵ�A����B����X�ύ�ڵ�C�����е�A����1��3���͵�B����3��n����
��1����գ�m���� ����n���� ����
��2����һ�κ����Ľ���ʽ����AOB�������
��3������ͼ��ش𣺵�xΪ��ֵʱ��kx+b��![]() ����ֱ��д���𰸣��� ����
����ֱ��д���𰸣��� ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com