
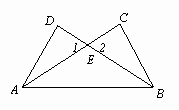
如图,AD⊥BD,BC⊥AC,AC=BD,求证:AD=BC,AE=BE.
|
因为AD⊥BD,BC⊥AC,所以∠C=∠D=90°,
在Rt△BAC和Rt△ABD中,
所以 Rt△BAC≌Rt△ABD(HL).所以 BC=AD. 在△ADE和△BCE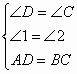 , ,
所以 △ADE≌△BCE(AAS).所以 AE=BE. |
|
要证 AD=BC,需要证明这两条线段所在的三角形全等,由于有垂直条件可以得到直角,进而想到用直角三角形全等的条件,观察图形发现AC=BD,又AB是公共边利用“HL”得到Rt△ABD≌Rt△BAC,进而得到AD=BC;进一步观察要证AE=BE,则需要证△ADE≌△BCE,虽然这两个都是直角三角形但是没有斜边相等的条件,因此不能用“HL”,所以只能用一般三角形全等的条件来证明,分析图中的边角关系,发现AD=BC,∠C=∠D=90°,又∠1=∠2,根据“AAS”可以证明△ADE≌△BCE,于是可以得到AE=BE. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com