
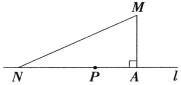
【题目】如图,一学校(点M)距公路(直线l)的距离(MA)为1km,在公路上距该校2km处有一车站(点N),该校拟在公路上建一个公交车停靠点(点p),以便于本校职工乘车上下班,要求停靠站建在AN之间且到此校与车站的距离相等,请你计算停靠站到车站的距离.
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
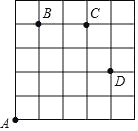
【题目】如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.
(1)图中A→C( , ),B→C( , ),C→ (+1,﹣2);
(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;
(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.
(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
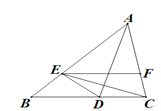
【题目】如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②EC平分∠DEF;③AD垂直平分CE.其中结论正确的有( )个
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG//CF;⑤S△FGC=3.6.其中正确结论是 . 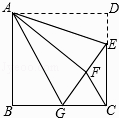
查看答案和解析>>
科目:初中数学 来源: 题型:
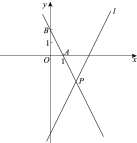
【题目】如图,在平面直角坐标系xOy中,直线![]() 的表达式为
的表达式为![]() ,点A,B的坐标分别为
,点A,B的坐标分别为
(1,0),(0,2),直线AB与直线![]() 相交于点P.
相交于点P.
(1)求直线AB的表达式;
(2)求点P的坐标;
(3)若直线![]() 上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
上存在一点C,使得△APC的面积是△APO的面积的2倍,直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y= ![]() 和y=
和y= ![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= ![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y= ![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA= ![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( ) 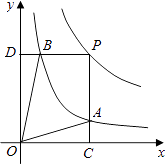
A.①②③
B.②③④
C.①③④
D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( ) 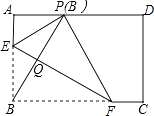
A.①②
B.②③
C.①③
D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com