
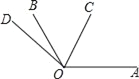
【题目】如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
(1)当t为何值时,射线OC与OD重合;
(2)当t为何值时,∠COD=90°;
(3)试探索:在射线OC与OD旋转的过程中,是否存在某个时刻,使得射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线?若存在,请求出所有满足题意的t的取值,若不存在,请说明理由.
【答案】(1)t=8min时,射线OC与OD重合;
(2)当t=2min或t=14min时,射线OC⊥OD;
(3)存在,详见解析.
【解析】
(1)当OC与OD重合时,根据角度关系可知∠AOC=∠AOB+∠BOD,利用题中射线的旋转速度,由角度=时间×旋转速度,列出方程,求解即可得到射线OC与OD重合时的时间t;
(2)当∠COD=90°时,可分为两种情况,当OC位于OD的右边时:∠BOD+120°=∠AOC+90°;当OC位于OD左边时:∠AOC-90°-120°=∠BOD,列出对应的方程,求解即可;
(3)分三种情况来考虑,当OB为角平分线时:120°-∠AOC=∠BOD;当OC为角平分线时:∠AOC-120°=![]() ∠BOD;当OD为角平分线时:∠AOC-120°=2∠BOD,列方程求解即可.
∠BOD;当OD为角平分线时:∠AOC-120°=2∠BOD,列方程求解即可.
解:(1)由题意得,20t=5t+120°,解得t=8,
即当t=8分钟时,射线OC与OD重合;
(2)当OC位于OD的右边时:∠BOD+120°=∠AOC+90°,则可得5t+120°=20t+90°,解得t=2分钟;
当OC位于OD左边时:∠AOC-90°-120°=∠BOD,则可得20t-90°-120°=5t,解得t=14分钟;
故当t=2或14分钟时,∠COD=90°;
(3)存在.
当OB为角平分线时:120°-∠AOC=∠BOD,则可得120°-20t=5t,解得t=4.8分钟;
当OC为角平分线时:∠AOC-120°=![]() ∠BOD,则可得20t-120°=
∠BOD,则可得20t-120°=![]() ×5t,解得t=
×5t,解得t=![]() 分钟;
分钟;
当OD为角平分线时:∠AOC-120°=2∠BOD,则可得20t -120°=2×5t,解得t=12分钟.
故当t=4.8或![]() 或12分钟时,射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线.
或12分钟时,射线OC,OB与OD中的某一条射线是另两条射线所夹角的角平分线.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】某开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。 请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。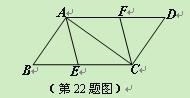
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距720km,一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是120km/h,慢车的速度是80km/h,快车到达乙地后,停留了20min,由于有新的任务,于是立即按原速返回甲地.在快车从甲地出发到回到甲地的整个程中,与慢车相遇了两次,这两次相遇时间间隔是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到这样一个问题:已知:在△ABC中,AB,BC,AC三边的长分别为![]() 、
、![]() 、
、![]() ,求△ABC的面积.
,求△ABC的面积.
小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积他把这种解决问题的方法称为构图法.
请回答:
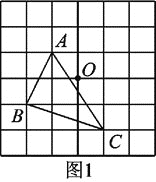

(1)①图1中△ABC的面积为________;
②图1中过O点画一条线段MN,使MN=2AB,且M、N在格点上.
(2)图2是一个6×6的正方形网格(每个小正方形的边长为1).利用构图法在图2中画出三边长分别为![]() 、2
、2![]() 、
、![]() 的格点△DEF.
的格点△DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
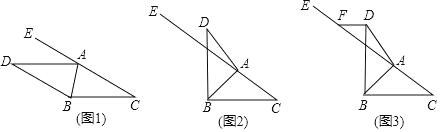
【题目】已知:点A在射线CE上,∠C=∠D.
(1)如图1,若AC∥BD,求证:AD∥BC;
(2)如图2,若∠BAC=∠BAD,BD⊥BC,请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图3,在(2)的条件下,过点D作DF∥BC交射线于点F,当∠DFE=8∠DAE时,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
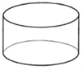
【题目】如图所示的圆柱形容器的容积为81升,它的底面直径是高的2倍.(π取3)
(1)这个圆柱形容器的底面直径为多少分米?
(2)若这个圆柱形容器的两个底面与侧面都是用铁皮制作的,则制作这个圆柱形容器需要铁皮多少平方分米?(不计损耗)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,以点A(1,0)为圆心,以2为半径的圆与x轴交于B,C两点,与y轴交于D,E两点.
(1)直接写出B,C,D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求出这个抛物线的解析式及它的顶点坐标.
(3)若圆A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,∠OMN=30°,试判断直线MN是否经过B、C、D三点所在抛物线的顶点?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 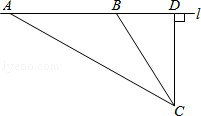
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.(参考数据: ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com