
分析 根据题意确定出m与n的值,已知等式右边通分并利用同分母分式的加法法则计算,确定出a,b,c的值即可.
解答 解:恒等式$\frac{ax-1}{(x-1)({x}^{2}+1)}$=$\frac{b}{x+m}$+$\frac{cx+5}{{x}^{2}+n}$中.$\frac{ax-1}{(x-1)({x}^{2}+1)}$和$\frac{cx+5}{{x}^{2}+n}$都是最简分式,且a,b,c,m,n都是常数,
可得m=-1,n=1,ax-1=b(x2+1)+(cx+5)(x-1)=(b+c)x2+(5-c)x+b-5,
∴b+c=0,5-c=a,b-5=-1,
解得:a=9,c=-4,b=4,
故答案为:-4;4;9
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(km)与行驶时间x(h)的关系如图所示,根据图象进行以下探究:
一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地,甲、乙两车到A地的距离y1、y2(km)与行驶时间x(h)的关系如图所示,根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.
甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,矩形OBAC的顶点A,B,C的坐标分别为(20,10),(20,0),(0,10).D为OA的中点,在线段OB上有一动点P,则当PA+PD为最小值时,点P的坐标是($\frac{40}{3}$,0).
如图,在平面直角坐标系中,矩形OBAC的顶点A,B,C的坐标分别为(20,10),(20,0),(0,10).D为OA的中点,在线段OB上有一动点P,则当PA+PD为最小值时,点P的坐标是($\frac{40}{3}$,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
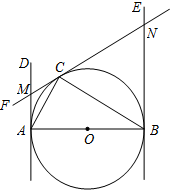 如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过 圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,求AM.
如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过 圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB.若∠ABC=30°,求AM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com