
【题目】如图,是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面宽8cm,水的最大深度为2cm,求该输水管的半径是多少? 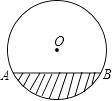
【答案】解:过点O做OC⊥AB于点D,连接OA.
设半径长为rcm,
∵OC⊥AB,
∴AD= ![]() AB
AB
= ![]() ×8
×8
=4(cm),
∵CD=2cm∴OD=r﹣2(cm)
在Rt△AOD中,由勾股定理得:(r﹣2)2+42=r2
r2﹣4r+4+42=42
4r=20
r=5,
答:该水管的半径是5cm.
【解析】先过点O作OD⊥AB于点D,连接OA,由垂径定理可知AD= ![]() AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
AB,设OA=r,则OD=r﹣2,在Rt△AOD中,利用勾股定理即可求出r的值.
【考点精析】通过灵活运用垂径定理的推论,掌握推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】在一只不透明的盒子里有背面完全相同,正面上分别写有数字1、2、3、4的四张卡片,小马从中随机地抽取一张,把卡片上的数字作为被减数;在另一只不透明的盒子里将形状、大小完全相同,分别标有数字1、2、3的三个小球混合后,小虎从中随机地抽取一个,把小球上的数字做为减数,然后计算出这两个数的差.
(1)请你用画树状图或列表的方法,求这两数差为0的概率;
(2)小马与小虎做游戏,规则是:若这两数的差为非正数,则小马赢;否则小虎赢.你认为该游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美化城市,改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。
(1)根据图中所提供的信息回答下列问题:2003年底的绿地面积为 公顷,比2002年底增加了 公顷;在2001年,2002年,2003年这三个中,绿地面积最多的是 年;
(2)为满足城市发展的需要,计划到2005年底使城区绿地面积达到72.6公顷,试04,05两绿地面积的年平均增长率。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,上七年级的小贝在一张纸上画了一条数轴,妹妹不知道它有什么用处,就在上面画了一只小猫和一只小狗,于是数轴上标的数字有的看不到了,请根据数轴回答下列问题:
(1)被小猫遮住的是正数还是负数?
(2)被小狗遮住的整数有几个?
(3)此时小猫和小狗之间(即点A,B之间)的整数有几个?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).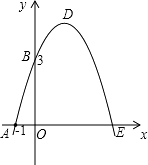
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)用适当的方法解方程:
①(x﹣2)2=2x﹣4
②x2﹣2x﹣8=0.
(2)先化简,再求值: ![]() ÷(
÷( ![]() ﹣a+1),其中a是方程x2﹣x=6的根.
﹣a+1),其中a是方程x2﹣x=6的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com