
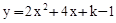 (k为正整数).
(k为正整数).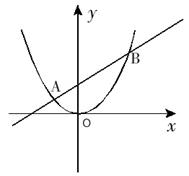
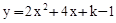 的图象与x轴有两个交点,求k的值.
的图象与x轴有两个交点,求k的值.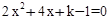 (k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数
(k为正整数)有两个不相等的整数解,点A(m,y1),B(m+1,y2),C(m+2,y3)都在二次函数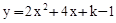 (k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.
(k为正整数)图象上,求使y1≤y2≤y3成立的m的取值范围.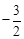 ;(3)(0,-4).
;(3)(0,-4).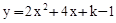 的图象与x轴有两个交点,知一元二次方程
的图象与x轴有两个交点,知一元二次方程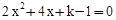 有两不相等的实数根,从而根的判别式大于0,解不等式求出正整数解即可;
有两不相等的实数根,从而根的判别式大于0,解不等式求出正整数解即可; 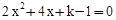 (k为正整数)有两个不相等的整数解得到k=1,从而得到函数解析式为
(k为正整数)有两个不相等的整数解得到k=1,从而得到函数解析式为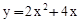 ,进而根据y1≤y2≤y3列不等式组求解即可;
,进而根据y1≤y2≤y3列不等式组求解即可;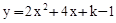 的图象与x轴有两个交点 ,
的图象与x轴有两个交点 ,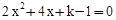 (k为正整数)有两个不相等的整数解,
(k为正整数)有两个不相等的整数解,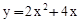 .
.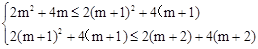 ,解得m≥
,解得m≥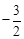 .
.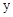 轴上,所以∠ACO=∠BCO,找A点关于y轴的对称点A ′(1,2),直线A ′B:y=6x-4,与y轴的交点即为所求C点,坐标为(0,-4).
轴上,所以∠ACO=∠BCO,找A点关于y轴的对称点A ′(1,2),直线A ′B:y=6x-4,与y轴的交点即为所求C点,坐标为(0,-4).

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
 (m是常数,
(m是常数, )与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.
)与x轴有两个不同的交点A、B,点A、点B关于直线x=1对称,抛物线的顶点为C.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.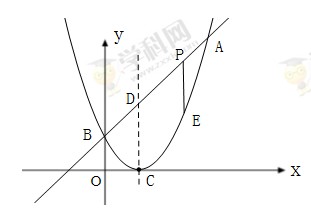
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,y3)三点,则y1、y2、y3的大小关系正确的是( )
,y3)三点,则y1、y2、y3的大小关系正确的是( )| A.y1>y2>y3 | B.y1>y3>y2 | C.y2>y1>y3 | D.y3>y1>y2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
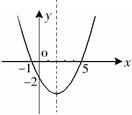
 时x的值只能取0
时x的值只能取0| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com