
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
【答案】
(1)解:设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50%)x=1.5x(米),
根据题意得: ![]() ,
,
解得:x=30,
当x=30时,1.5x≠0,
∴x=30是分式方程的解,
1.5x=45,
答:工程队在使用新设备后每天能修路45米
(2)解:设修建这条公路的总费用为W元,
则W=16000m+25000n,
∵30m+45n=1500,
∴m= ![]() ,
,
把m= ![]() 代入W=16000m+25000n得;
代入W=16000m+25000n得;
W=16000× ![]() +25000n=800000+1000n,
+25000n=800000+1000n,
∵k=1000>0,
∴W随n的增大而增大,
∵16≤n≤26,
∴当n=16时,W有最小值,最小值为;800000+16000=816000(元),
m= ![]() =26,
=26,
答:当m=26,n=16时,修建这条公路的总费用最少,最少费用为816000元
【解析】(1)设使用旧设备每天能修路x米,则使用新设备后每天能修路(1+50%)x=1.5x(米),根据一直使用旧设备完成工程的工作时间-先使用旧设备后使用新设备完成工程的工作时间=15列出方程,求解检验即可;
(2)设修建这条公路的总费用为W元,根据W=使用旧设备的花费+使用新设备的花费,列出函数关系式,然后根据使用旧设备的工作量+使用新设备的工作量=1500,列出方程,然后用含n的式子表示m,再将该式子代入函数解析式,从而得到:W=800000+1000n,此函数中W随N的增大而增大又,16≤n≤26,故当n=16时,W有最小值,最小值为;800000+16000=816000(元),进而算出m,得出答案。
【考点精析】掌握一次函数的性质和分式方程的应用是解答本题的根本,需要知道一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数 ![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 . 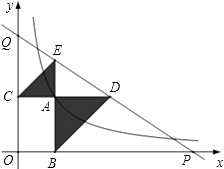
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() +(﹣1)2017﹣(
+(﹣1)2017﹣(![]() ﹣
﹣![]() ),
),
(2)2(3a2b﹣2ab2)﹣3(ab2+2a2b),
(3)﹣7x2y﹣3xy2+5x2y+13xy,其中x=﹣![]() ,y=
,y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店在某一时间以每件a元(a>0)的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%.
(1)当a=60时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?
(2)小安发现:不论a为何值,这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )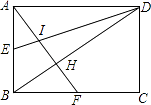
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在A的左侧),嘉嘉进行如下作图:

①以点O为圆心,OC为半径画弧,交OB于点D,连接CD
②以点A为圆心,OC为半径画弧MN,交AP于点M
③以点M为圆心,CD为半径画弧,交MN于点E,连接ME,作射线AE
如图所示,则下列结论不成立的是( )
A. CD∥EM B. AE∥OB C. ∠ODC=∠AEM D. ∠OAE=∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角” (如图)就是一例.这个三角形给出了![]() (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着
展开式中各项的系数;第五行的五个数1,4,6,4,1,恰好对应着![]() 展开式中各项的系数,等等.
展开式中各项的系数,等等.

有如下三个结论:
①当a=1,b=1时,代数式![]() 的值是1;
的值是1;
②当a=-1,b=2时,代数式![]() 的值是1;
的值是1;
③当代数式![]() 的值是1时,a的值是-2或-4.
的值是1时,a的值是-2或-4.
上述结论中,所有正确结论的序号为( )
A. ①② B. ② C. ③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量校园内一棵不可攀的树的高度,数学应用实践小组做了如下的探索实践:根据《物理学》中光的反射定律,利用一面镜子和一根皮尺,设计如图的测量方案:把镜子放在离树(AB)9米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.8米,则树(AB)的高度为米.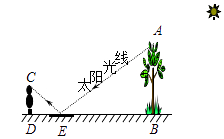
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com