
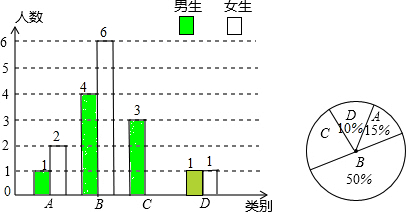
���� ��1������A��ѧ����������A��ѧ����ռ�ٷֱȿɵõ���ѧ������������ѧ��������ȥA��B��D��ѧ�������ټ�ȥC��ѧ�����������ɵ�C��Ů������
��2�����ݣ�1�������C��Ů������ͼ���ɣ�
��3�����Ȼ�����״ͼ�������ɵô𰸣�
��� �⣺��1�������ѧ������3��15%=20��
C������20-3-10-3-2=2��
�ʴ�Ϊ��20��2��
��2����ͼ��ʾ��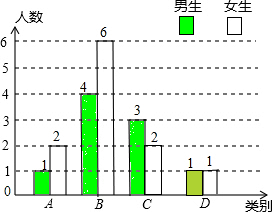 ��
��
��3��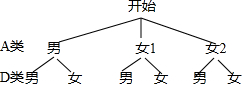 ��
��
����״ͼ�ɵù���6�ֿ��ܵĽ��������ǡ��һ����ͬѧ��һ��Ůͬѧ�Ľ����3�У�����ǡ����һ����ͬѧ��һ��Ůͬѧ�ĸ����ǣ�$\frac{3}{6}$=$\frac{1}{2}$��
���� ������Ҫ����������ͳ��ͼ���Լ����ʣ��ؼ������ո���=������������������֮�ȣ�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
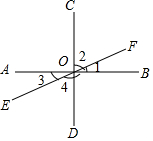 ��ͼ��AB��CD������ΪO��ֱ��EF������O��
��ͼ��AB��CD������ΪO��ֱ��EF������O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com