
����Ŀ����ͼ��������y1��ax2��bx��c(a��0)ͼ���һ���֣������ߵĶ�������A(1��3)����x���һ������B(4��0)��ֱ��y2��mx��n(m��0)�������߽���A��B���㣬���н��ۣ���2a��b��0����abc>0���۷���ax2��bx��c��3��������ȵ�ʵ����������������x�����һ��������(��1��0)������1<x<4ʱ����y2<y1��������ȷ���ǣ���
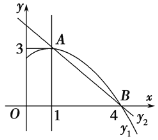
A.�٢ܢ�B.�٢ۢܢ�C.�٢ۢ�D.�٢ڢ�
���𰸡�C
��������
�ٸ��ݶԳ���x=1��ȷ��a��b�Ĺ�ϵ��Ȼ���ж����ɣ�
�ڸ���ͼ��ȷ��a��b��c�ķ��ţ������ж���
�۷���ax2+bx+c=3�ĸ�����y=3��ͼ���������߽���ĺ������ж����ɣ�
�ܸ��ݶԳ����жϼ��ɣ�
����ͼ��ɵã���1<x<4ʱ������������ֱ�ߵ����棬��y2<y1��
�⣺�١߶Գ���Ϊ��x=1��
��![]() ��a=-2b,��2a+b=0���ʢ���ȷ;
��a=-2b,��2a+b=0���ʢ���ȷ;
�������߿�������
��a��0
���Գ�����y���Ҳ࣬
��b��0
����������y�ύ��������
��c��0
��abc<0,�ʢڲ���ȷ��
�������ߵĶ�������A��1,3��
���ax2+bx+c=3��������ȵ�ʵ������x=1���ʢ���ȷ��
�������߶Գ����ǣ�x=1��B��4,0����
����������x�����һ�������ǣ�-2,0���ʢܴ���
��ͼ��ã���1<x<4ʱ����y2<y1���ʢ���ȷ��
�ʴ�ΪC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
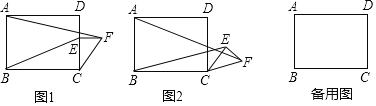
����Ŀ����ͼ1���ھ���ABCD�У�AB��6��BC��8����E�DZ�CD�ϵĵ㣬��CE��4������E��CD�Ĵ��ߣ����ڴ����Ͻ�ȡEF��3������CF������CEF�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊa��
��1�����ⷢ��
��a��0��ʱ��AF���� ��BE���� ��![]() ���� ��
���� ��
��2����չ̽��
���жϣ���0���a�㣼360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2���������֤����
�Ĵ�С���ޱ仯�������ͼ2���������֤����
��3��������
����CEF��ת��A��E��F���㹲��ʱ��ֱ��д���߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��������������Ϸ����Ϸ������:��һ�δ�����A��������ش���B��C�����е�ijһ��,�Ժ��ÿһ�δ��������ϴεĴ���������ش������������е�ijһ�ˣ�
(1)�����δ������ǡ��B���еĸ���; (������ͼ���б���ʾ���п��ܵĽ��)
(2)�����δ������ǡ��A���еĸ��ʣ� (������ͼ���б���ʾ���п��ܵĽ��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
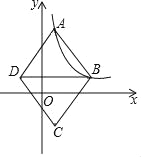
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��B�ڷ���������y=![]() ��k��0��x��0����ͼ���ϣ�������ֱ�Ϊ1��4���Խ���BD��x�ᣮ������ABCD�����Ϊ
��k��0��x��0����ͼ���ϣ�������ֱ�Ϊ1��4���Խ���BD��x�ᣮ������ABCD�����Ϊ![]() ����k��ֵΪ_____��
����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ʽΪy=(m-2) ![]()
��1��������Ϊ��������������˵������y��x�������С
��2��������Ϊ���κ�����д����������ʽ����д�����ڷ���
��3��������Ϊ������������д����������ʽ����˵�������ڵڼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1����PΪBC������һ�㣨�����B��C�غϣ����ֱ��B��C��D������AP�Ĵ��ߣ�����ֱ���B�䡢C�䡢D�䣬��BB�䣫CC�䣫DD�����Сֵ�ǣ�������
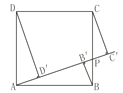
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() ��ֱ��
��ֱ��![]() ��y�ύ�ڵ�A����˫����
��y�ύ�ڵ�A����˫����![]() ���ڵ�
���ڵ�![]() ��
��
��1�����B�����꼰k��ֵ��
��2����ֱ��ABƽ�ƣ�ʹ����x�ύ�ڵ�C����y�ύ�ڵ�D����![]() �����Ϊ6����ֱ��CD�ı���ʽ��
�����Ϊ6����ֱ��CD�ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2+bx+c��������B����4��0���͵�A��1��0������y�ύ�ڵ�C��
��1��ȷ�������ߵı���ʽ�������C�����ꣻ
��2����ͼ1���������ϴ���һ��E��ʹ��ACE����ACΪֱ�DZߵ�ֱ�������Σ�����������������ĵ�E���ꣻ
��3����ͼ2��M��N���������ϵ������㣨��M�ڵ��N��ࣩ���ֱ����M��N��PM��x�ᣬPN��y�ᣬPM��PN���ڵ�P����M��N�˶�ʱ��ʼ�ձ���MN��![]() ���䣬����MNP������ֱ�DZ߳��ɶ�����ϵʱ����ֱ��д��ֱ��MN�ı���ʽ��
���䣬����MNP������ֱ�DZ߳��ɶ�����ϵʱ����ֱ��д��ֱ��MN�ı���ʽ��
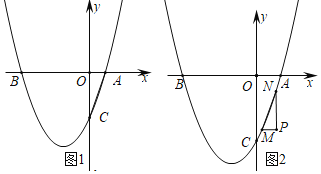
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com