练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    设点的坐标（，），其中横坐标可取－1，2，纵坐标可取－1， 1，2，

    （1）求出点的坐标的所有等可能结果（用树形图或列表法求解）；

    （2）求点与点（1，－1）关于原点对称的概率。


    【解析】

    试题分析：列举出所有情况，让所求的情况数除以总情况数即为所求的概率．

    （1）如图所示：

    ∴点A的坐标，所求可能结果有6种，分别是（－1，－1）、

    （－1，1）、（－1，2）、（2，－1）、（2，1）、（2，2）；

    （2）点A与点B（1，－1）关于原点对称的只有一种（－1，1）为事件A，。

    考点：本题考查的是概率公式

    点评：用到的知识点为：概率=所求情况数与总情况数之比．两点关于原点对称，横纵坐标均互为相反数．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中放置一直角三角板，其顶点为A（-1，0），B（0，
    		3
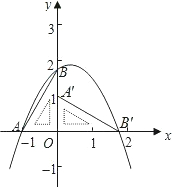    ），精英家教网O（0，0），将此三角板绕原点O顺时针旋转90°，得到△A′B′O．
    （1）如图，一抛物线经过点A，B，B′，求该抛物线解析式；
    （2）设点P是在第一象限内抛物线上一动点，求使四边形PBAB′的面积达到最大时点P的坐标及面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直角梯形ABCD的腰BC所在直线的解析式为y=-
    		3
    x-6
    		3
    ，点A与坐标原点O重合，点D的坐标为（0，-4
    		3
    ），将直角梯形ABCD绕点O顺时针旋转180°，得到直角梯形OEFG（如图1）．
    （1）直接写出E，F两点的坐标及直角梯形OEFG的腰EF所在直线的解析式；
    （2）将图1中的直角梯形ABCD先沿x轴向右平移到点A与点E重合的位置，再让直角顶点A紧贴着EF，向上平移直角梯形ABCD（即梯形ABCD向上移动时，总保持着AB∥FG），当点A与点F重合时，梯形ABCD停止移动．观察得知：在梯形ABCD移动过程中，其腰BC始终经过坐标原点O．（如图2）
    ①设点A的坐标为（a，b），梯形ABCD与梯形OEFG重合部分的面积为S，试求a与何值时，S的值恰好等于梯形OEFG面积的
    5
    16
    ；
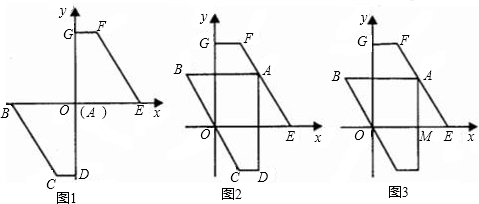
    ②当点A在EF上滑动时，设AD与x轴的交点为M，试问：在y轴上是否存在点P，使得△PAM是底角为30°的等腰三角形？如果存在，请求出所有符合条件的点P的坐标；如果不存在，请说明理由．（利用图3进行探索）精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，函数y=-
    12
    x+2    的图象交y轴于M，交x轴于N，点P是直线MN上任意一点，PQ⊥x轴，Q是垂足，设点Q的坐标为（t，0），△POQ的面积为S（当点P与M、N重合时，其面积记为0）．
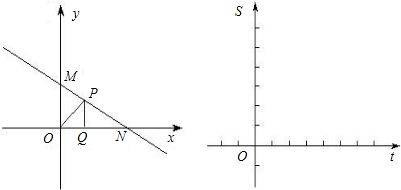
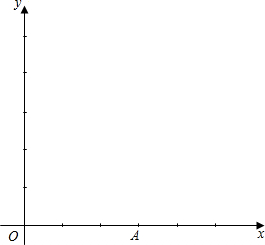    精英家教网
    （1）试求S与t之间的函数关系式；
    （2）在如图所示的直角坐标系内画出这个函数的图象，并利用图象求使得S=a（a＞0）的点P的个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在直角坐标系中，点A的坐标是（3，0），点P在第一象限内的直线y=-x精英家教网+4上．设点P的坐标为（x，y）．
    （1）在所给的坐标系中画出直线y=-x+4；
    （2）求△POA的面积S与变量x的函数关系式，并写出自变量x的取值范围；
    （3）当S=
    92
    时，求点P的坐标，画出此时的△POA，并用尺规作图法，作出其外接圆（保留作图痕迹，不写作法）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

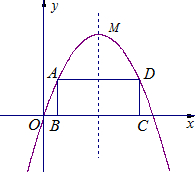    如图，已知抛物线y=-x2+bx+9-b2（b为常数）经过坐标原点O，且与x轴交于另一点E精英家教网．其顶点M在第一象限．
    （1）求该抛物线所对应的函数关系式；
    （2）设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B，DE⊥x轴于点C．
    ①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；
    ②求矩形ABCD的周长的最大值，并写出此时点A的坐标；
    ③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断并说明理由．

    查看答案和解析>>

    同步练习册答案